Câu hỏi:
3 năm trước
Cho tam giác $ABC$ cân tại $A,$ trung tuyến $AM.$ Gọi $I$ là trung điểm của $AC,{\rm{ }}K$ là điểm đối xứng với $M$ qua $I.$
Tìm điều kiện của tam giác $ABC$ để tứ giác $AMCK$ là hình vuông?
Trả lời bởi giáo viên
Đáp án đúng: c
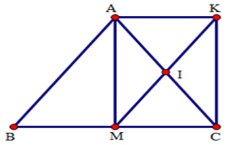
Theo câu trước thì \(AKCM\) là hình chữ nhật.
Để hình chữ nhật $AMCK$ là hình vuông thì $AM = MC$
Mà $AM$ là đường trung tuyến của tam giác cân $ABC$
\( \Rightarrow AM = MC = \dfrac{1}{2}BC \Rightarrow \) Tam giác $ABC$ vuông cân tại $A.$
Hướng dẫn giải:
+ Để $AMCK$ là hình vuông ta dựa vào dấu hiệu hình chữ nhật có hai cạnh bên bằng nhau là hình vuông, từ đó suy ra điều kiện của tam giác $ABC.$

