Câu hỏi:
2 năm trước
Cho tam giác $ABC$ cân tại $A$. Gọi $D,E$ theo thứ tự thuộc các cạnh bên $AB,AC$ sao cho $AD{\rm{ }} = {\rm{ }}AE$ .
Tứ giác $BDEC$ là hình gì?
Trả lời bởi giáo viên
Đáp án đúng: c
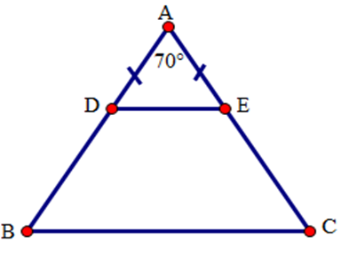
Tam giác $ADE$ có \(AD = AE(gt)\) nên tam giác $ADE$ cân tại $A$.
Suy ra \(\widehat {ADE} = \widehat {AED} = \left( {180^\circ - \widehat {DAE}} \right):2\;\left( 1 \right)\)
Tam giác $ABC$ cân tại $A$ (gt) nên \(\widehat {ABC} = \widehat {ACB} = \left( {180^\circ - \widehat {BAC}} \right):2\;\;\;\;\left( 2 \right)\)
Từ (1) và (2) suy ra \(\widehat {ADE} = \widehat {ABC}\)
Mà 2 góc \(\widehat {ADE}\) và \(\widehat {ABC}\) là hai góc ở vị trí đồng vị nên suy ra $DE{\rm{//}}BC$
Tứ giác $BDEC$ có DE // BC nên tứ giác $BDEC$ là hình thang.
Lại có \(\widehat {ABC} = \widehat {ACB}\) (vì tam giác \(ABC\) cân tại \(A\) ) nên \(BDEC\) là hình thang cân.
Hướng dẫn giải:
Bước 1: Ta sử dụng tính chất tam giác cân để chứng minh hai góc đồng vị bằng nhau. Suy ra \(DE{\rm{//}}BC\) nên \(DECB\) là hình thang.
Bước 2: Sử dụng dấu hiệu nhận biết: Hình thang có hai góc ở đáy bằng nhau là hình thang cân để suy ra \(DECB\) là hình thang cân.
