Cho tam giác \(ABC\) cân tại \(A\) có: \(\widehat A = {100^0}, BC = a, AC = b.\) Về phía ngoài tam giác \(ABC\) vẽ tam giác \(ABD\) cân tại \(D\) có: \(\widehat {ADB} = {140^0}.\) Tính chu vi tam giác \(ABD\) theo \(a\) và \(b.\)

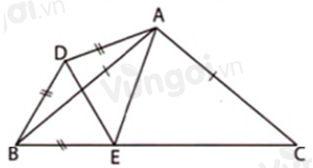
Trên cạnh \(BC\) lấy điểm \(E\) sao cho \(BE = BD.\)

\(\Delta ABC\) cân tại \(A\) nên \(\widehat {ABC} = \dfrac{{{{180}^o} - \widehat {BAC}}}{2} = \dfrac{{{{180}^o} - {{100}^o}}}{2} = {40^o}.\)

\(\Delta ABD\) cân tại \(D\) nên \(\widehat {DBA} = \dfrac{{{{180}^o} - \widehat {ADB}}}{2} = \dfrac{{{{180}^o} - {{140}^o}}}{2} = {20^o}\).

Ta có: \(\widehat {DBE} = \widehat {DBA} + \widehat {ABC} = {20^o} + {40^o} = {60^o}.\)

Xét \(\Delta BDE\) có: \(\widehat {DBE} = {60^o}\) nên \(\Delta BDE\) đều, suy ra \(BD = BE = DE = DA.\)

\(\widehat {EDA} = \widehat {BDA} - \widehat {BDE} = {140^o} - {60^o} = {80^o}\)

\(\Delta DAE\) cân tại \(D\) (vì \(DA = DE\,(cmt)\)) nên \(\widehat {DEA} = \widehat {DAE} = \dfrac{{{{180}^o} - \widehat {EDA}}}{2} = \dfrac{{{{180}^o} - {{80}^o}}}{2} = {50^o}.\)

\(\widehat {EAC} = \widehat {DAB} + \widehat {BAC} - \widehat {DAE} = {20^o} + {100^o} - {50^o} = {70^o}.\)

\(\widehat {AEC} = {180^o} - \widehat {DEA} - \widehat {DEB} = {180^o} - {50^o} - {60^o} = {70^o}.\)

\(\Delta CAE\) có \(\widehat {EAC} = \widehat {AEC} = {70^o}\) nên \(\Delta CAE\) cân tại \(C\), suy ra \(AC = EC.\)

Do đó: \(AD = BD = BE = BC - EC = BC - AC = a - b.\)

            \(AB = AC = b.\)

Vậy chu vi của \(\Delta ABD\) là:

\(AD + BD + AB = a - b + a - b + b = 2a - b.\)