Câu hỏi:
2 năm trước
Cho tam giác $ABC$. Các tia phân giác của các góc \(B\) và \(C\) cắt nhau tại \(I\). Qua \(I\) kẻ đường thẳng song song với $BC$, cắt các cạnh $AB,AC$ lần lượt tại $D$ và $E$.
Chọn khẳng định đúng.
Trả lời bởi giáo viên
Đáp án đúng: b
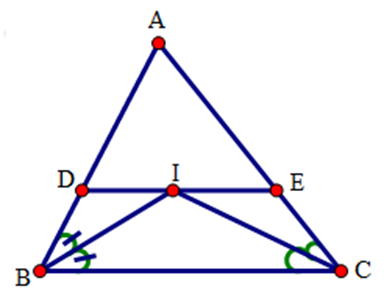
Vì $DE//BC$ (gt) nên suy ra \(\widehat {DIB} = \widehat {IBC}\) ( so le trong)
Mà \(\widehat {DBI} = \widehat {IBC}\) (gt) nên \(\widehat {DIB} = \widehat {DBI}\)
Suy ra tam giác $BDI$ cân đỉnh $D$.
Do đó \(DI = DB\,\,(1)\)
Ta có: $IE//CB$ nên suy ra \(\widehat {EIC} = \widehat {BCI}\) ( so le trong)
Mà \(\widehat {BCI} = \widehat {ECI}\) (gt) nên \(\widehat {ECI} = \widehat {EIC}\)
Suy ra tam giác $EIC$ cân đỉnh $E$.
Do đó \(EI = EC\,\,(2)\).
Cộng (1) và (2) vế theo vế ta được:
\(DI + EI = BD + CE \Rightarrow DE = BD + CE\)
Hướng dẫn giải:
Ta sử dụng tính chất các cạnh của tam giác cân.
