Câu hỏi:
2 năm trước
Cho (O;4) có dây AC bằng cạnh hình vuông nội tiếp và dây BC bằng cạnh tam giác đều nội tiếp đường tròn đó ( điểm C và A nằm cùng phía với BO ). Tính số đo góc ACB
Trả lời bởi giáo viên
Đáp án đúng: d
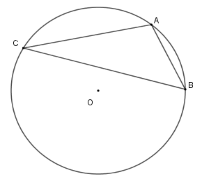
+ Vì AC bằng cạnh của hình vuông nội tiếp (O) nên số đo cung AC=90∘
Vì BC bằng cạnh của tam giác đều nội tiếp (O) nên số đo cung BC=120∘
Từ đó suy ra số đo cung AB=120∘−90∘=30∘
+ Vì ^ACB là góc nội tiếp chắn cung AB nên ^ACB=30∘2=15∘
Hướng dẫn giải:
+ Tìm số đo các cung BC và AB để tìm số đo cung AC
+ Sử dụng: số đo góc nội tiếp bằng nửa số đo cung bị chắn

