Cho hình vuông \(ABCD\) có cạnh bằng \(1\). Hai điểm \(M\), \(N\) thay đổi lần lượt ở trên cạnh \(AB\), \(AD\) sao cho \(AM = x\left( {0 \le x \le 1} \right)\), \(DN = y\left( {0 \le y \le 1} \right)\). Tìm mối liên hệ giữa \(x\) và \(y\) sao cho \(CM \bot BN\).
Trả lời bởi giáo viên
Chọn hệ trục tọa độ \(Oxy\) như hình vẽ.
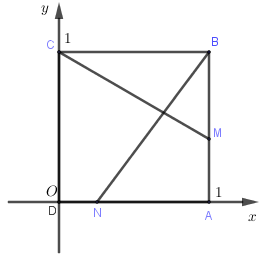
Khi đó: \(D\left( {0;0} \right),C\left( {1;0} \right),A\left( {0;1} \right);B\left( {1;1} \right),M\left( {x;1} \right);N\left( {0;y} \right)\).
Ta có: \(\overrightarrow {CM} = \left( {x - 1;1} \right)\); \(\overrightarrow {BN} = \left( { - 1;y - 1} \right)\)
Do đó: \(CM \bot BN \Leftrightarrow \overrightarrow {CM} .\overrightarrow {BN} = 0 \Leftrightarrow x - y = 0\).
Hướng dẫn giải:
- Gắn hệ trục tọa độ, tìm tọa độ các điểm và véc tơ tương ứng.
- \(CM \bot BN \Leftrightarrow \overrightarrow {CM} .\overrightarrow {BN} = 0\).




