Trả lời bởi giáo viên
Đáp án đúng: c
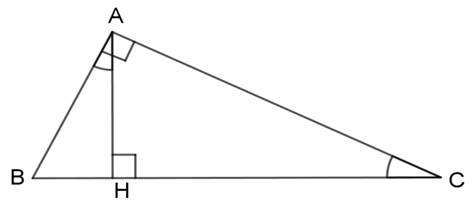
Xét 2 tam giác vuông AHB và CHA có: \widehat {BAH} = \widehat {ACH} (gt)
\Rightarrow \Delta AHB\backsim\Delta CHA\;(g - g)
\Rightarrow A đúng.
Xét 2 tam giác vuông AHC và BAC có:
\widehat C chung
\Rightarrow \Delta AHC\backsim\Delta BAC\;(g - g)
\Rightarrow D đúng.
Xét hai tam giác vuông \Delta BAH và \Delta BCA có:
\widehat B chung
\widehat {BAH} = \widehat {BCA}\left( {gt} \right)
\Rightarrow \Delta BAH \backsim \Delta BCA\left( {g - g} \right) nên B đúng, C sai.
Hướng dẫn giải:
- Áp dụng lý thuyết về các trường hợp đồng dạng của tam giác vuông để chứng minh các cặp tam giác vuông đồng dạng với nhau, từ đó chọn đáp án đúng.
Câu hỏi khác
- Bài tập định lý Ta-lét. Định lý đảo và hệ quả của định lý Ta-lét toán 8 có lời giải
- Bài tập tính chất đường phân giác của tam giác toán 8 có lời giải
- Bài tập trường hợp đồng dạng thứ nhất toán 8 có lời giải
- Bài tập hai tam giác đồng dạng toán 8 có lời giải
- Bài tập trường hợp đồng dạng thứ hai toán 8 có lời giải
