Câu hỏi:
2 năm trước
Cho hình thang vuông $ABCD$ có \(\hat A = \hat D = 90^\circ ,\;AB = AD = 2cm,\;DC = 4cm.\) Tính góc \(ABC\) của hình thang.
Trả lời bởi giáo viên
Đáp án đúng: d
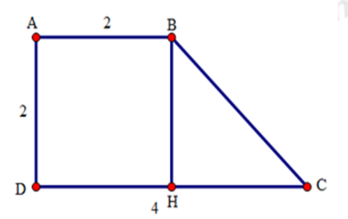
Từ $B$ kẻ $BH$ vuông góc với $CD$.
Tứ giác $ABHD$ là hình thang có hai cạnh bên \(AD{\rm{//}}BH\) nên \(AD = BH,AB = DH\) .
Mặt khác, \(AB = AD = 2cm\) nên suy ra \(BH = DH = 2cm\) .
Do đó: \(HC = DC - HD = 4 - 2 = 2cm\) .
Tam giác $BHC$ có \(BH = HC = 2cm\) nên tam giác $BHC$ cân đỉnh $H$.
Lại có \(\widehat {BHC} = 90^\circ \) (do $BH \bot CD$) nên tam giác $BHC$ vuông cân tại $H$.
Do đó \(\widehat {BCH} = \left( {180^\circ - \widehat {BHC}} \right):2 = \left( {180^\circ - 90^\circ } \right):2 = 45^\circ \)
Xét hình thang $ABCD$ có:
\(\widehat {ABC} = 360^\circ - \left( {\hat A + \hat D + \hat C} \right) = 360^\circ - \left( {90^\circ + 90^\circ + 45^\circ } \right) = 135^\circ .\)
Vậy \(\widehat {ABC} = 135^\circ \) .
Hướng dẫn giải:
Ta sử dụng tính chất hình thang, hình thang vuông và định lý về tổng các góc trong tứ giác.
