Cho hình thang $ABCD\left( {AB//CD} \right),{\rm{ }}M$ là trung điểm của $AD,{\rm{ }}N$ là trung điểm của $BC.$ Gọi $I,{\rm{ }}K$ theo thứ tự là giao điểm của $MN$ với $BD,{\rm{ }}AC.$ Cho biết $AB = 6cm,{\rm{ }}CD = 14cm.$ Tính độ dài $MI,{\rm{ }}IK.$

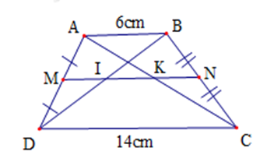
- Hình thang $ABCD$ có:

$\left. \begin{array}{l}{\rm{AM}} = {\rm{MD(gt)}}\\{\rm{BN}} = {\rm{NC (gt)}}\end{array} \right\} \Rightarrow $$MN$  là đường trung bình của hình thang $ABCD.$

\( \Rightarrow \) $MN//AB//CD$ (tính chất).

- Tam giác $ABD$ có:  $\left. \begin{array}{l}{\rm{AM }} = {\rm{ MD}}\\MI//AB\end{array} \right\} \Rightarrow $$ID = IB$  (định lý đảo về đường trung bình của tam giác).

\( \Rightarrow \) $MI$ là đường trung bình của $\Delta ADB$ $ \Rightarrow MI = \dfrac{1}{2}AB = \dfrac{1}{2}.6 = 3(cm)$

- Tương tự tam giác \(ACD\)  có: $AM = MD,{\rm{ }}MK//DC$ nên $AK = KC,$ hay ${\rm{ }}MK$ là đường trung bình của tam giác $ACD$, ta có:

$MK = \dfrac{1}{2}CD = \dfrac{1}{2}.14 = 7(cm)$

\( \Rightarrow \) $IK = MK - MI = 7 - 3 = 4\left( {cm} \right)$

Vậy \(MI = 3cm;IK = 4cm.\)