Câu hỏi:
2 năm trước
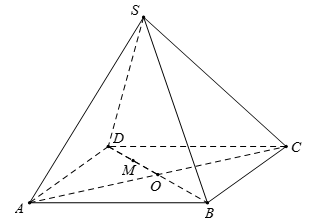
Cho hình chóp $S.ABCD,O$ là điểm nằm bên trong tam giác $ACD$. Thiết diện của hình chóp cắt bởi \(mp\left( \alpha \right)\) đi qua $O$ và song song với $AC$ và $SD$ có số cạnh bằng:
Trả lời bởi giáo viên
Đáp án đúng: c
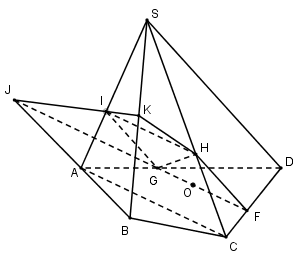
Trong $\left( {ABCD} \right)$ qua $O$ kẻ \(GF//AC\left( {G \in AD,F \in CD} \right)\)
Trong $\left( {SCD} \right)$ qua $F$ kẻ \(FH//SD\left( {H \in SC} \right)\)
\( \Rightarrow \left( \alpha \right)\) là $\left( {GFH} \right)$ .
\(\left( \alpha \right) \cap \left( {ABCD} \right) = GF,\left( \alpha \right) \cap \left( {SCD} \right) = HF.\)
Ta có: \(\left( \alpha \right)\) và $\left( {SAC} \right)$ có $H$ chung, \(\left( \alpha \right) \supset GF,\left( {SAC} \right) \supset AC,GF//AC\).
\( \Rightarrow \) Qua $H$ kẻ \(HI//AC\left( {I \in SA} \right)\)
\( \Rightarrow \left( \alpha \right) \cap \left( {SAC} \right) = HI,\left( \alpha \right) \cap \left( {SAD} \right) = GI\).
Trong $\left( {ABCD} \right)$ gọi \(J = GF \cap AB \Rightarrow J \in AB \Rightarrow J \in \left( {SAB} \right)\)
Trong $\left( {SAB} \right)$ gọi \(K = IJ \cap SB\left( {K \in SB} \right)\)
\( \Rightarrow \left( \alpha \right) \cap \left( {SAB} \right) = IK,\left( \alpha \right) \cap \left( {SBC} \right) = HK\)
Vậy thiết diện của hình chóp cắt bởi \(mp\left( \alpha \right)\) là $GFHKI$ là đa giác có $5$ cạnh.
Hướng dẫn giải:
- Từ những giả thiết ban đầu xác định \(mp\left( \alpha \right)\).
- Dựng thiết diện của \(mp\left( \alpha \right)\) với hình chóp.
