Cho hình chóp \(S.ABCD\) có \(SA \bot \left( {ABCD} \right)\), đáy \(ABCD\) là hình vuông cạnh \(2a\),\(SA = 2a\sqrt[{}]{3}\). Gọi \(I\) là trung điểm của \(AD\), mặt phẳng \(\left( P \right)\) qua \(I\) và vuông góc với \(SD\). Tính diện tích thiết diện của hình chóp cắt bởi mặt phẳng \(\left( P \right)\).
Trả lời bởi giáo viên
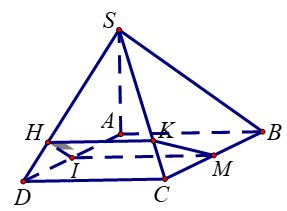
Kẻ \(IM{\rm{//}}CD\) với \(M \in BC\).
Ta có \(\left. \begin{array}{l}IM \bot SA\\IM \bot AD\end{array} \right\}\)\( \Rightarrow IM \bot \left( {SAD} \right)\)\( \Rightarrow IM \bot SD\)\( \Rightarrow \left( P \right) \cap \left( {ABCD} \right) = IM\).
Kẻ \(IH \bot SD\) với \(H \in SD\)\( \Rightarrow \left( P \right) \cap \left( {SAD} \right) = IH\).
Vì \(\left. \begin{array}{l}IM{\rm{//}}CD\\IM \subset \left( P \right)\\CD \subset \left( {SCD} \right)\end{array} \right\}\)\( \Rightarrow \left( P \right) \cap \left( {SCD} \right) = HK\) với \(HK{\rm{//}}IM\left( {{\rm{//}}CD} \right)\)và \(K \in SC\).
\(\left( P \right) \cap \left( {SBC} \right) = KM\).
Vì \(IM \bot \left( {SAD} \right)\) nên \(IM \bot IH\). Do đó thiết diện của hình chóp cắt bởi mặt phẳng \(\left( P \right)\) là hình thang \(IHKM\) vuông tại \(I\)và \(H\).
Ta có \(IM = AB = 2a\).
Xét \(\Delta SAD\) có: \(\tan \widehat {SAD} = \dfrac{{SA}}{{AD}}\)\( = \dfrac{{2\sqrt[{}]{3}a}}{{2a}}\)\( = \sqrt[{}]{3}\)\( \Rightarrow \widehat {SDA} = 60^\circ \).
Xét \(\Delta DHI\) có: \(\sin \widehat {HDI} = \dfrac{{HI}}{{ID}}\)\( \Rightarrow HI = ID.\sin 60^\circ \)\( = a.\dfrac{{\sqrt[{}]{3}}}{2}\).
Xét \(\Delta SAD\) có: \(SD = \sqrt[{}]{{S{A^2} + A{D^2}}}\)\( = \sqrt[{}]{{12{a^2} + 4{a^2}}}\)\( = 4a\).
Xét \(\Delta DHI\) có: \(HD = \sqrt[{}]{{I{D^2} - I{H^2}}}\)\( = \sqrt[{}]{{{a^2} - \dfrac{{3{a^2}}}{4}}}\)\( = \dfrac{a}{2}\)\( \Rightarrow SH = SD - HD\)\( = 4a - \dfrac{a}{2}\)\( = \dfrac{{7a}}{2}\).
Vì \(HK{\rm{//}}CD\) nên theo Talet ta có \(\dfrac{{HK}}{{CD}} = \dfrac{{SH}}{{SD}}\)\( = \dfrac{{\dfrac{{7a}}{2}}}{{4a}} = \dfrac{7}{8}\)\( \Rightarrow HK = \dfrac{7}{8}CD\)\( = \dfrac{7}{8}.2a\)\( = \dfrac{{7a}}{4}\).
Do đó diện tích thiết diện là \({S_{IHKM}} = \dfrac{{\left( {IM + HK} \right).IH}}{2}\)\( = \dfrac{{\left( {2a + \dfrac{{7a}}{4}} \right).\dfrac{{a\sqrt[{}]{3}}}{2}}}{2}\)\( = \dfrac{{15\sqrt[{}]{3}{a^2}}}{{16}}\).
Hướng dẫn giải:
- Xác định thiết diện cắt bởi \(\left( P \right)\).
- Nhận xét tính chất thiết diện và tính diện tích

