Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình chữ nhật, \(SA \bot \left( {ABCD} \right)\). Gọi \(AE;AF\) lần lượt là các đường cao của tam giác \(SAB\) và tam giác $SAD$. Gọi \(M\) là giao điểm của \(SC\) với \( (AEF) \). Chọn khẳng định đúng trong các khẳng định sau ?
Trả lời bởi giáo viên
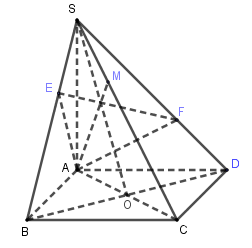
Ta có: \(\left\{ \begin{array}{l}AB \bot BC\\SA \bot BC\end{array} \right. \Rightarrow BC \bot \left( {SAB} \right) \Rightarrow BC \bot AE.\)
Vậy: \(\left\{ \begin{array}{l}AE \bot SB\\AE \bot BC\end{array} \right. \Rightarrow AE \bot SC\left( 1 \right)\)
Tương tự : \(AF \bot SC\left( 2 \right)\)
Từ \(\left( 1 \right);\left( 2 \right) \Rightarrow SC \bot \left( {AEF} \right).\)
Mà \(AM \subset \left( {AEF} \right)\) nên \(AM \bot SC\).
Hướng dẫn giải:
Sử dụng điều kiện đường thẳng vuông góc với mặt phẳng để chứng minh \(SC \bot \left( {AEF} \right).\)
Giải thích thêm:
Các em cũng có thể xác định vị trí cụ thể của \(M\) rồi chứng minh, việc này giúp các em củng cố lại kiến thức chương trước đã học về xác định thiết diện, tuy nhiên trình bày bài sẽ khá dài.

