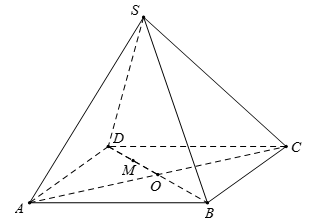
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình bình hành, mặt bên \(SAB\) là tam giác vuông tại \(A\), \(SA = a\sqrt 3 \), \(SB = 2a\). Điểm \(M\) nằm trên đoạn \(AD\) sao cho \(AM = 2MD\). Gọi \(\left( P \right)\) là mặt phẳng qua \(M\) và song song với \(\left( {SAB} \right)\). Tính diện tích thiết diện của hình chóp cắt bởi mặt phẳng \(\left( P \right)\).

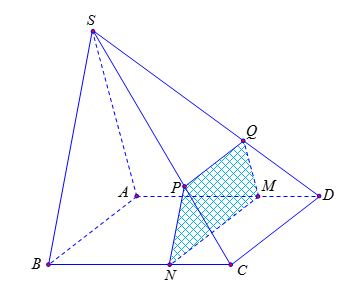
Ta có:

¦ \(\left\{ \begin{array}{l}\left( P \right)\,\,{\rm{//}}\,\left( {SAB} \right)\\M \in AD,\,M \in \left( P \right)\end{array} \right.\) \( \Rightarrow \left\{ \begin{array}{l}\left( P \right) \cap \left( {ABCD} \right) = MN\\\left( P \right) \cap \left( {SCD} \right) = PQ\end{array} \right.\) và \(MN\,{\rm{//}}\,PQ\,{\rm{//}}\,AB\) (1)

¦ \(\left\{ \begin{array}{l}\left( P \right)\,\,{\rm{//}}\,\left( {SAB} \right)\\M \in AD,\,M \in \left( P \right)\end{array} \right.\) \( \Rightarrow \left\{ \begin{array}{l}\left( P \right) \cap \left( {SAD} \right) = MQ\\\left( P \right) \cap \left( {SBC} \right) = NP\end{array} \right.\) và \(\left\{ \begin{array}{l}MQ\,{\rm{//}}\,SA\\NP\,{\rm{//}}\,SB\end{array} \right.\)

Mà tam giác \(SAB\) vuông tại \(A\) nên \(SA \bot AB\) \( \Rightarrow MN \bot MQ\) (2)

Từ (1) và (2) suy ra \(\left( P \right)\) cắt hình chóp theo thiết diện là hình thang vuông tại \(M\) và \(Q\).

Mặt khác

¦ \(MQ\,{\rm{//}}\,SA\) \( \Rightarrow \dfrac{{MQ}}{{SA}} = \dfrac{{DM}}{{DA}} = \dfrac{{DQ}}{{DS}}\) \( \Rightarrow MQ = \dfrac{1}{3}SA\) và \(\dfrac{{DQ}}{{DS}} = \dfrac{1}{3}\).

¦ \(PQ\,{\rm{//}}\,CD\) \( \Rightarrow \dfrac{{PQ}}{{CD}} = \dfrac{{SQ}}{{SD}}\) \( \Rightarrow PQ = \dfrac{2}{3}AB\), với \(AB = \sqrt {S{B^2} - S{A^2}}  = a\)

Khi đó \({S_{MNPQ}} = \dfrac{1}{2}MQ.\left( {PQ + MN} \right)\) \( \Leftrightarrow {S_{MNPQ}} = \dfrac{1}{2}\dfrac{{SA}}{3}.\left( {\dfrac{{2AB}}{3} + AB} \right)\)\( \Leftrightarrow {S_{MNPQ}} = \dfrac{{5{a^2}\sqrt 3 }}{{18}}\).