Cho hình chóp đều $S.ABCD$ có tất cả các cạnh bằng $a$. Gọi $M$ là trung điểm $SC$. Tính góc $\varphi $ giữa hai mặt phẳng $\left( {MBD} \right)$ và $\left( {ABCD} \right)$.
Trả lời bởi giáo viên
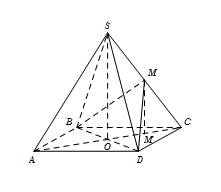
Gọi M’ là trung điểm $OC \Rightarrow MM'\parallel SO \Rightarrow MM' \bot \left( {ABCD} \right).$
Theo công thức diện tích hình chiếu, ta có ${S_{\Delta \,M'BD}} = \cos \varphi .{S_{\Delta \,MBD}}$
$\begin{array}{l} \Rightarrow \cos \varphi = \dfrac{{{S_{\Delta \,M'BD}}}}{{{S_{\Delta \,MBD}}}} = \dfrac{{BD.M'O}}{{BD.MO}} = \dfrac{{M'O}}{{MO}} = \dfrac{{\dfrac{1}{2}OC}}{{\dfrac{1}{2}SA}}\\ = \dfrac{{\sqrt {B{C^2} - O{B^2}} }}{{SA}} = \dfrac{{\sqrt {{a^2} - {{\left( {\dfrac{{a\sqrt 2 }}{2}} \right)}^2}} }}{a} = \dfrac{{\sqrt 2 }}{2} \Rightarrow \varphi = {45^0}.\end{array}$
Hướng dẫn giải:
Sử dụng phương pháp xác định góc giữa hai mặt phẳng và áp dụng các hệ thức lượng trong tam giác vuông

