Cho hình bình hành \(ABCD\) có $DC = 2BC$. Gọi $E,F$ là trung điểm của $AB,DC$. Gọi $AF$ cắt $DE$ tại $I,{\rm{ }}BF$ cắt $CE$ tại $K.$

Tứ giác $EIFK$ là hình gì?

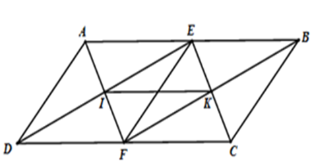
Theo câu trước ta có tứ giác \(BEDF\)  là hình bình hành nên \(ED = BF;\,ED//BF \Rightarrow EI//FK\,\left( 1 \right)\)

Theo câu trước ta có tứ giác \(AEDF\) và \(BEFC\)   là hình thoi nên \(I;K\) lần lượt là trung điểm của \(DE\) và \(BF\)

Suy ra \(EI = \dfrac{{DE}}{2};\,FK = \dfrac{{BF}}{2}\)  mà \(DE = BF\left( {cmt} \right) \Rightarrow EI = FK\,\,\left( 2 \right)\)

Từ (1) và (2) suy ra tứ giác \(EIFK\)  là hình bình hành.

Mà \(AEDF\)  là hình thoi nên \(AF \bot DE\)  (tính chất hình thoi)\( \Rightarrow \widehat {EIF} = 90^\circ \)

Hình bình hành \(EIFK\) có một góc vuông \(\widehat {EIF} = 90^\circ \)  nên \(EIFK\) là hình chữ nhật.