Câu hỏi:
2 năm trước
Cho hình bình hành \(ABCD\) có $DC = 2BC$. Gọi $E,F$ là trung điểm của $AB,DC$. Gọi $AF$ cắt $DE$ tại $I,{\rm{ }}BF$ cắt $CE$ tại $K.$
Chọn câu đúng nhất.
Trả lời bởi giáo viên
Đáp án đúng: d
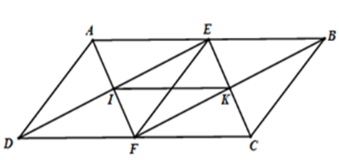
Xét hình bình hành \(ABCD\) có \(E;F\) lần lượt là trung điểm của \(AB;CD\); \(DC = 2BC\) nên
\(AE = EB = BC = CF = DF = AD\) ;\(AB//CD;\,AD//BC\)
Xét tứ giác \(DEBF\) có \(\left\{ \begin{array}{l}EB//DF\\EB = DF\end{array} \right.\) nên \(DEBF\) là hình bình hành (dhnb)
Xét tứ giác \(AEFD\) có \(AE = DF;AE//DF\) nên \(AEFD\) là hình bình hành (dhnb), lại có \(AE = AD\) nên hình bình hành \(AEFD\) là hình thoi.
Tương tự ta cũng có \(EBCF\) là hình thoi. Nhận thấy chưa đủ điều kiện để \(EBCF\) là hình vuông.
Nên A, B đúng, C sai.
Hướng dẫn giải:
+ Chỉ ra các cặp cạnh song song và bằng nhau
+ Sử dụng các dấu hiệu nhận biết hình bình hành, hình thoi, hình vuông
