Câu hỏi:
2 năm trước
Cho hình bình hành $ABCD$ có $BC = 2AB\;$ và $\widehat A = 60^\circ $ . Gọi $E,F\;$ theo thứ tự là trung điểm của $BC$ và $AD.$ Gọi $I$ là điểm đối xứng với $A$ qua $B.$
Tứ giác $BICD$ là hình gì?
Trả lời bởi giáo viên
Đáp án đúng: a
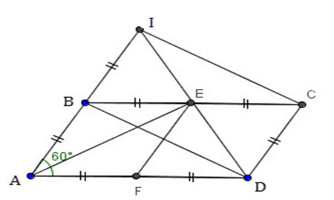
Do $AB//CD$ (giả thiết) nên $BI//CD$
Mặt khác $BI = AB$ (giả thiết); $AB = CD$ (giả thiết)
$ \Rightarrow BI = CD$
Vậy $BICD$ là hình bình hành (dhnb) (1)
Theo giả thiết ta có \(BI = AB = AF = FD \Rightarrow AI = AD\) mà \(\widehat {IAD} = 60^\circ \) (gt) nên tam giác \(ADI\) đều.
Xét tam giác $ADI$ đều có $BD$ là trung tuyến đồng thời là đường cao.
$ \Rightarrow \widehat {DBI} = 90^\circ $ (2)
Từ (1) và (2) suy ra $BICD$ là hình chữ nhật (dấu hiệu nhận biết).
Hướng dẫn giải:
+ Chứng minh \(BICD\) là hình bình hành
+ Tìm thêm tính chất của \(BICD\) để sử dụng dấu hiệu hình bình hành có một góc vuông
