Cho hàm số $y = {x^4} - 2m{x^2} + {m^2} + m.$ Tất cả các giá trị của $m$ để đồ thị hàm số có $3$ điểm cực trị tạo thành tam giác có một góc ${120^o}$ là:
Trả lời bởi giáo viên
\(\begin{array}{l}y' = 4{x^3} - 4mx\\y' = 0 \Leftrightarrow 4{x^3} - 4mx = 0 \Leftrightarrow 4x\left( {{x^2} - m} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = \pm \sqrt m \end{array} \right.\end{array}\)
Điều kiện để hàm số có $3$ cực trị: \(m > 0\)
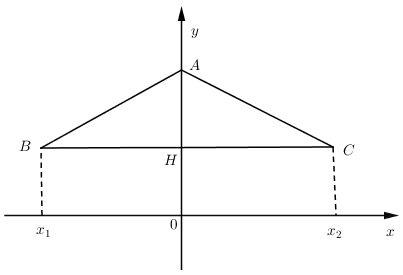
\(\begin{array}{l}x = 0 \Rightarrow A\left( {0;\,{m^2} + m} \right)\\x = - \sqrt m \Rightarrow y = {\left( { - \sqrt m } \right)^4} - 2m{\left( { - \sqrt m } \right)^2} + {m^2} + m \\= {m^2} - 2{m^2} + {m^2} + m = m \Rightarrow B\left( { - \sqrt m ;\,m} \right)\\x = \sqrt m \Rightarrow C\left( {\sqrt m ;\,m} \right)\end{array}\)
$\begin{array}{l}
\overrightarrow {AB} = \left( { - \sqrt m ; - {m^2}} \right),\overrightarrow {AC} = \left( {\sqrt m ; - {m^2}} \right)\\
\widehat {BAC} = {120^0}\\
\Leftrightarrow \dfrac{{\overrightarrow {AB} .\overrightarrow {AC} }}{{\left| {\overrightarrow {AB} } \right|.\left| {\overrightarrow {AC} } \right|}} = \cos {120^0}\\
\Leftrightarrow \dfrac{{ - m + {m^4}}}{{\sqrt {m + {m^4}} .\sqrt {m + {m^4}} }} = - \dfrac{1}{2}\\
\Leftrightarrow 2\left( {{m^4} - m} \right) = - \left( {m + {m^4}} \right)\\
\Leftrightarrow 3{m^4} - m = 0\\
\Leftrightarrow m\left( {3{m^3} - 1} \right) = 0\\
\Leftrightarrow \left[ \begin{array}{l}
m = 0\left( {loai} \right)\\
m = \dfrac{1}{{\sqrt[3]{3}}}
\end{array} \right.
\end{array}$
Hướng dẫn giải:
- Bước 1: Tính $y'$.
- Bước 2: Ba điểm cực trị $A,B,C$ trong đó $A\left( {0;c} \right)$ tạo thành tam giác cân có góc ở đỉnh bằng $\alpha $ cho trước$ \Leftrightarrow \dfrac{{\overrightarrow {AB} .\overrightarrow {AC} }}{{\left| {\overrightarrow {AB} }\right|.\left| {\overrightarrow {AC} } \right|}} = \cos \alpha $
- Bước 3: Kết luận.

