Câu hỏi:
2 năm trước
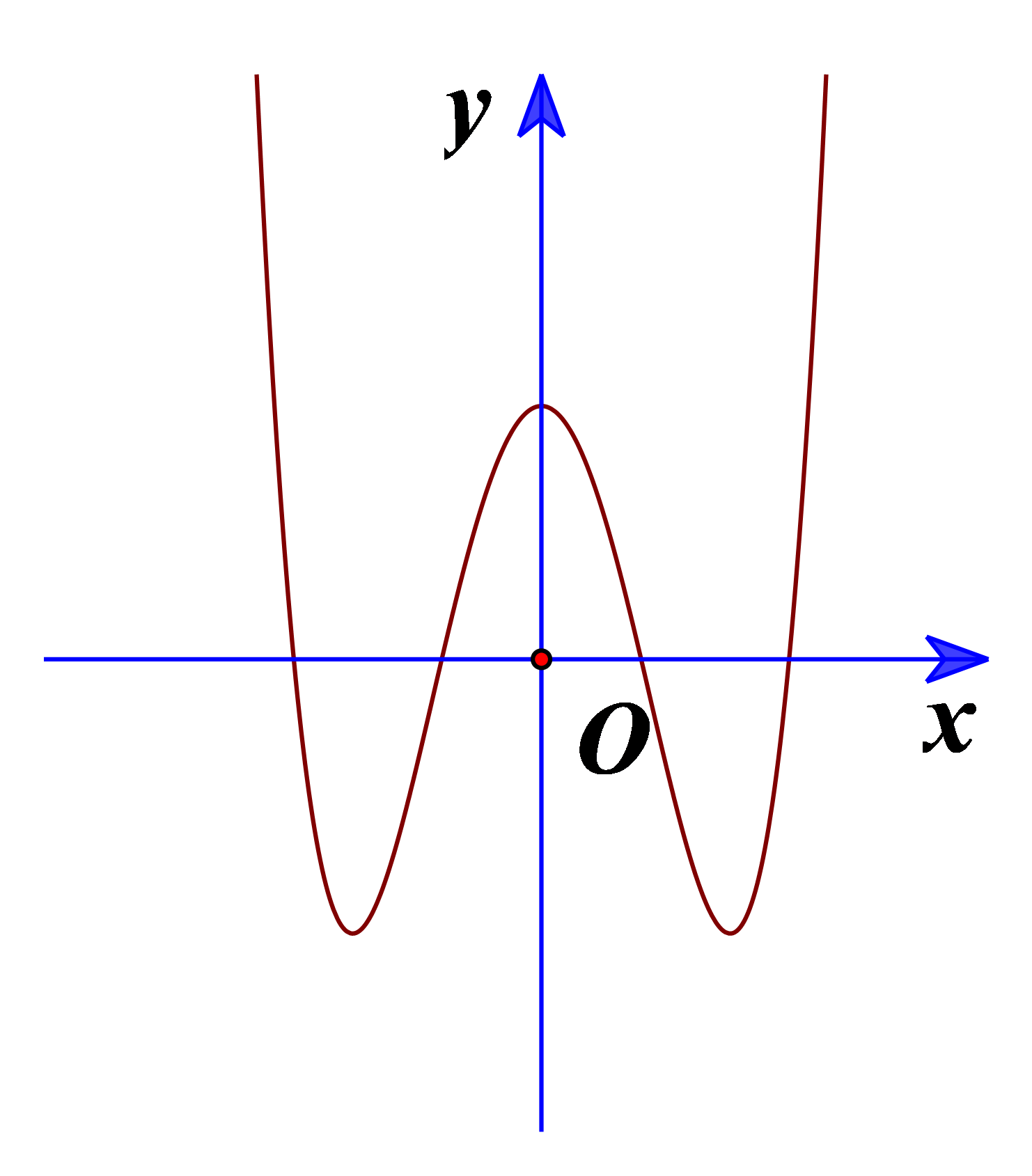
Cho hàm số \(y = (a - 1){x^4} + (b + 2){x^2} + c - 1\) có đồ thị như hình vẽ bên. Mệnh đề nào dưới đây là đúng?
Trả lời bởi giáo viên
Đáp án đúng:
\(a > 1,b < - 2,c > 1\).
Đồ thị đi lên khi \(x \to + \infty \) nên \(a - 1 > 0 \Leftrightarrow a > 1\).
Đồ thị đi qua điểm \((0;c - 1)\) có tung độ nằm phía trên trục hoành nên \(c - 1 > 0 \Leftrightarrow c > 1\).
Đồ thị hàm số có 3 điểm cực trị nên \((a - 1) \cdot (b + 2) < 0\) mà \(a > 1\) nên \(b + 2 < 0 \Leftrightarrow b < - 2\).
Hướng dẫn giải:
- Xét đồ thị khi \(x \to + \infty \) và đánh giá \(a - 1\).
- Giao điểm đồ thị với trục tung có tung độ là \(c - 1\).
- Dựa vào số điểm cực trị để đánh giá b.