Cho đường tròn $(O).$ Từ một điểm $M$ ở ngoài $(O)$, vẽ hai tiếp tuyến $MA$ và $MB$ sao cho góc $AMB$ bằng ${120^0}$. Biết chu vi tam giác $MAB$ là $6\left( {3 + 2\sqrt 3 } \right)cm$, tính độ dài dây $AB.$
Trả lời bởi giáo viên
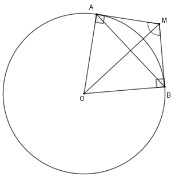
Xét $\left( O \right)$ có $MA = MB$; $\widehat {AMO} = \widehat {BMO}$ (tính chất hai tiếp tuyến cắt nhau)
Nên $\widehat {AMO} = 60^\circ $. Xét tam giác vuông $AOM$ có $AM = AO.cot\widehat {AMO} = \dfrac{{R\sqrt 3 }}{3}$ nên $MA = MB = \dfrac{{R\sqrt 3 }}{3}$
Lại có $\widehat {AOB} + \widehat {AMB} = 180^\circ \Rightarrow \widehat {AOB} = 60^\circ $ suy ra $\Delta AOB$ là tam giác đều $ \Rightarrow AB = OB = OA = R$
Chu vi tam giác $MAB$ là $MA + MB + AB = \dfrac{{R\sqrt 3 }}{3} + \dfrac{{R\sqrt 3 }}{3} + R = 6\left( {3 + 2\sqrt 3 } \right)$
$ \Leftrightarrow R\left( {\dfrac{{3 + 2\sqrt 3 }}{3}} \right) = 6\left( {3 + 2\sqrt 3 } \right) \Rightarrow R = 18\,cm$ nên $AB = 18\,cm$.
Hướng dẫn giải:
Sử dụng tính chất hai tiếp tuyến cắt nhau và công thức chu vi tam giác
Câu hỏi khác
- Đề kiểm tra giữa học kì 1 - đề số 1 Toán 9 có lời giải chi tiết
- Đề kiểm tra giữa học kì 1 - đề số 2 Toán 9 có lời giải chi tiết
- Đề kiểm tra giữa học kì 1 - đề số 3 Toán 9 có lời giải chi tiết
- Đề kiểm tra giữa học kì 2 - đề số 1 Toán 9 có lời giải chi tiết
- Đề kiểm tra giữa học kì 2 - đề số 2 Toán 9 có lời giải chi tiết
