Câu hỏi:
3 năm trước
Cho đường tròn $(O)$ đường kính $AB$ và đường tròn $(O')$ đường kính $AO$. Các điểm $C,D$ thuộc đường tròn $(O)$ sao cho $B \in $ cung $CD$ và cung $BC$ nhỏ hơn cung $BD$. Các dây cung $AC$ và $AD$ cắt đường tròn $(O')$ theo thứ tự $E$ và $F$.
So sánh dây $AE$ và $AF$ của đường tròn $(O')$.
Trả lời bởi giáo viên
Đáp án đúng: a
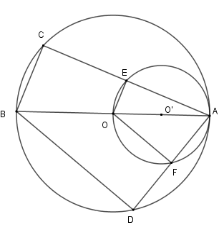
Theo định lý Pytago ta có : $A{E^2} = A{O^2} - O{E^2}$ và $A{F^2} = A{O^2} - O{F^2}$ mà $OE < OF$
$ \Rightarrow A{E^2} > A{F^2} \Rightarrow AE > AF$.
Hướng dẫn giải:
Sử dụng định lý Pytago

