Cho đường tròn (O) bán kính R ngoại tiếp tam giác ABC có ba góc nhọn. Các tiếp tuyến của đường tròn (O) tại các điểm B, C cắt nhau tại điểm P. Gọi D, E tương ứng là chân các đường vuông góc hạ từ P xuống  các đường thẳng AB, AC và M là trung điểm cạnh BC.

Khi tam giác $ABC$ là tam giác đều. Hãy tính diện tích tam giác $ADE$ theo $R.$

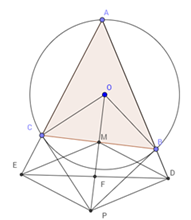
\(\Delta ABC\;\;\)đều, khi đó $A,{\rm{ }}O,{\rm{ }}M,{\rm{ }}F$ thẳng hàng, $AF$ vuông góc với $DE$ tại $F.$\( \Rightarrow \)  \({S_{\Delta ADE}}\) $ = \dfrac{1}{2}DE.AF$

\(\Delta ABC\;\;\)đều nên ta có: $\widehat {CAB} = {60^0}$ mà $\widehat {CBP} = \widehat {CAB} = {60^0}$(góc nội tiếp và góc tạo bởi tia tiếp tuyến và dây cung cùng chắn cung BC)

\( \Rightarrow AM = MP;MF = \dfrac{1}{2}MP\)

 có \(AB = \;\sqrt {A{M^2} + \;M{B^{2\;}}} \) \( \Rightarrow AB = R\sqrt 3 \)

\(OA = R \Rightarrow AM = \dfrac{3}{2}OA = \dfrac{3}{2}R \Rightarrow AF = \dfrac{3}{2}R + \dfrac{3}{4}R = \dfrac{9}{4}R\)

\(\Delta ABC\;\;\backsim\;\Delta ADE\)  \( \Rightarrow \)  \(\dfrac{{BC}}{{DE}} = \dfrac{{AM}}{{AF}} = \dfrac{2}{3} \Rightarrow DE = \dfrac{{3\sqrt 3 }}{2}R\)

\( \Rightarrow {S_{\Delta ADE}} = \dfrac{1}{2}DE.AF = \dfrac{{27\sqrt 3 }}{{16}}{R^2}\) .