Cho đa thức \(f(x) = {x^4} - 3{{\rm{x}}^3} + 3{{\rm{x}}^2} + {\rm{ax}} + b\) và đa thức \(g(x) = {x^2} - 3{\rm{x}} + 4\). Biết \(f\left( x \right)\) chia hết cho \(g\left( x \right)\) . Khi đó tích \(a.b\) bằng
Trả lời bởi giáo viên
Ta có
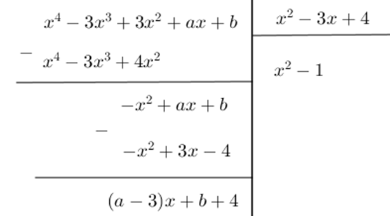
Phần dư của phép chia $f\left( x \right)$ cho \(g\left( x \right)\) là \(R = \left( {a - 3} \right)x + b + 4\) . Để phép chia trên là phép chia hết thì \(R = 0,\forall x \Leftrightarrow \left( {a - 3} \right)x + b + 4 = 0,\,\forall x \Leftrightarrow \left\{ \begin{array}{l}a - 3 = 0\\b + 4 = 0\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}a = 3\\b = - 4\end{array} \right. \Rightarrow ab = - 12\) .
Hướng dẫn giải:
+ Sử dụng cách chia đa thức một biến đã sắp xếp.
+ Sử dụng nhận xét: Nếu phép chia có phần dư \(R = 0\) thì phép chia đó là phép chia hết.
Chú ý: \(Ax + B = 0\) với \(\forall x \Leftrightarrow \left\{ \begin{array}{l}A = 0\\B = 0\end{array} \right.\) .
Giải thích thêm:
Một số em có thể nhân nhầm dấu ở bước cuối dẫn đến sai đáp án.