Cho \(\Delta ABC\) vuông tại \(A,\) các cạnh \(AB,\,\,AC\) tương ứng tỉ lệ với \(3\) và \(4.\) Biết đường cao \(AH = 18\,\,cm.\)

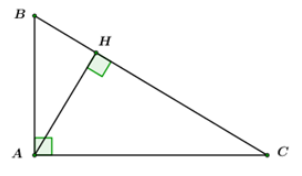
Tính chu vi \(\Delta ABC\).

Theo đề bài ta có: các cạnh \(AB,\,\,AC\) tương ứng tỉ lệ với \(3\) và \(4\)

\( \Rightarrow \dfrac{{AB}}{{AC}} = \dfrac{3}{4} \Leftrightarrow AB = \dfrac{3}{4}AC.\)

Áp dụng hệ thức lượng trong \(\Delta ABC\) vuông tại \(A\)  có đường cao \(AH\) ta có:

\(\begin{array}{l}\dfrac{1}{{A{H^2}}} = \dfrac{1}{{A{B^2}}} + \dfrac{1}{{A{C^2}}} \Leftrightarrow AH = \dfrac{{AB.AC}}{{\sqrt {A{B^2} + A{C^2}} }}\\ \Leftrightarrow 18 = \dfrac{{\dfrac{3}{4}AC.AC}}{{\sqrt {\dfrac{9}{{16}}A{C^2} + A{C^2}} }} = \dfrac{{\dfrac{3}{4}A{C^2}}}{{\dfrac{5}{4}AC}} = \dfrac{3}{5}AC\\ \Leftrightarrow AC = \dfrac{{18.5}}{3} = 30\,\,cm.\\ \Rightarrow AB = \dfrac{3}{4}AC = \dfrac{3}{4}.30 = 22,5\,\,cm.\end{array}\)

Áp dụng định lý Pitago cho \(\Delta ABC\) vuông tại \(A\) ta có:

\(BC = \sqrt {A{B^2} + A{C^2}}  = \sqrt {22,{5^2} + {{30}^2}}  = 37,5\,\,cm.\)

\( \Rightarrow \) Chu vi \(\Delta ABC:\,\,\,AB + BC + CA = 22,5 + 30 + 37,5 = 90\,\,cm.\)