Cho \(\Delta ABC\) có \({90^0} > \widehat B > \widehat C\). Kẻ \(AH \bot BC\left( {H \in BC} \right)\). Gọi $M$ là một điểm nằm giữa $H$ và $B,$ $N$ thuộc tia đối của tia $CB.$
Chọn câu đúng.
Trả lời bởi giáo viên
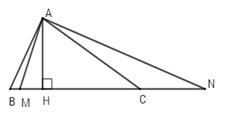
Vì $M$ nằm giữa $B$ và $H$ \( \Rightarrow HM < HB\) .
Mà $HM$ và $HB$ tương ứng là hình chiếu của $AM$ và $AB$ trên $BC$
$ \Rightarrow AM < AB\left( 2 \right)$ (quan hệ giữa đường xiên và hình chiếu).
Vì $N$ thuộc tia đối của tia $CB$ thì suy ra \(HN > HC\). Mà $HN$ và $HC$ tương ứng là hình chiếu của $AN$ và $AC$ trên $BC$ \( \Rightarrow AC < AN\left( 3 \right)\) (quan hệ giữa đường xiên và hình chiếu).
Từ \(\left( 1 \right)\left( 2 \right)\left( 3 \right) \Rightarrow AM < AB < AN.\)
Hướng dẫn giải:
Áp dụng các định lý sau:
Quan hệ giữa đường xiên và hình chiếu.
Quan hệ giữa góc và cạnh trong tam giác.


