Câu hỏi:
2 năm trước
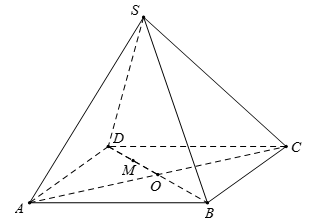
Cho chóp tứ giác $S.ABCD$ có hai đường chéo $AC$ và $BD$. Gọi $E$ và $F$ lần lượt là giao điểm của $AB$ và $CD,AD$ và $BC$ . Một mặt phẳng \(\left( \alpha \right)\) đi qua điểm $M$ trên cạnh $SB$ ($M$ nằm giữa $S$ và $B$ ) song song với $SE$ và $SF$ ($SE$ không vuông góc với $SF$). Thiết diện của hình chóp cắt bởi \(mp\left( \alpha \right)\) có số cạnh là:
Trả lời bởi giáo viên
Đáp án đúng: b
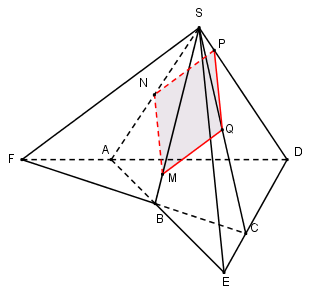
Giả sử thiết diện cần tìm đi qua điểm \(M \in SB.\)
Trong $\left( {SAB} \right)$ qua $M$ kẻ \(MN//SE\left( {N \in SA} \right)\) ta có:
\(\left( \alpha \right)\) và $\left( {SAB} \right)$ có điểm $M$ chung.
\(\begin{array}{l}\left( \alpha \right)//SE \subset \left( {SAB} \right)\\MN//SE\\ \Rightarrow \left( \alpha \right) \cap \left( {SAB} \right) = MN.\end{array}\)
Tương tự trong $\left( {SAD} \right)$ qua $N$ kẻ \(NP//SF\left( {P \in SD} \right)\) ta có: \(\left( \alpha \right) \cap \left( {SAD} \right) = NP.\)
Trong $\left( {SCD} \right)$ kẻ \(PQ//SE\left( {Q \in SC} \right)\) ta có: \(\left( \alpha \right) \cap \left( {SCD} \right) = PQ.\)
\(\left( \alpha \right) \cap \left( {SBC} \right) = MQ.\)
Vậy thiết diện của hình chóp khi cắt bởi \(mp\left( \alpha \right)\) là tứ giác $MNPQ$.
Hướng dẫn giải:
- Đưa về cùng mặt phẳng.
- Sử dụng các yếu tố song song.
- Xác định thiết diện của hình chóp dựa vào các yếu tố song song.
