Câu hỏi:
2 năm trước
Bốn điện tích q = 3.10-7C giống nhau đặt tại 4 đỉnh của hình vuông. Phải đặt một điện tích q0 nằm ở đâu và bằng bao nhiêu để năm điện tích này cân bằng
Trả lời bởi giáo viên
Đáp án đúng: a
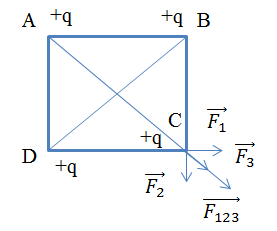
- 3 điện tích tại 3 đỉnh tác dụng vào điện tích q ở C
\(\overrightarrow {{F_1}} + \overrightarrow {{F_2}} + \overrightarrow {{F_3}} = \overrightarrow {{F_{123}}} \)
Ta có: \(\overrightarrow {{F_{123}}} \) có phương thuộc đường chéo của hình vuông
Để q0 cân bằng: 4 điện tích tương đương với q0 cân bằng với q ở C
\(\overrightarrow {{F_0}} + \overrightarrow {{F_{123}}} = 0 \to \overrightarrow {{F_0}} = - \overrightarrow {{F_{123}}} \)
Tương tự q0 đặt trên đường chéo BD
=> Để năm điện tích cân bằng => q0 là giao điểm của AC và BD.
Muốn \(\overrightarrow {{F_0}} \)trực đối với \(\overrightarrow {{F_{123}}} \)=> q0 < 0
- Mặt khác:
\(\begin{array}{l}{F_0} = {F_{123}}{\rm{ (1)}}\\{F_0} = k\frac{{\left| {q{q_0}} \right|}}{{O{C^2}}} = k\frac{{\left| {q{q_0}} \right|}}{{{{(a\frac{{\sqrt 2 }}{2})}^2}}} = k\frac{{\left| {q{q_0}} \right|}}{{{a^2}}}2{\rm{ (2)}}\\\left\{ \begin{array}{l}{F_1} = {F_2} = k\frac{{{q^2}}}{{{a^2}}}\\{F_{12}} = \sqrt {{F_1}^2 + {F_2}^2} = {F_1}\sqrt 2 = k\frac{{{q^2}}}{{{a^2}}}\sqrt 2 \end{array} \right.\\{F_3} = k\frac{{{q^2}}}{{A{C^2}}} = k\frac{{{q^2}}}{{{{(a\sqrt 2 )}^2}}} = k\frac{{{q^2}}}{{2{{\rm{a}}^2}}}\\{F_{123}} = {F_{12}} + {F_3} = k\frac{{{q^2}}}{{{a^2}}}\sqrt 2 + k\frac{{{q^2}}}{{2{{\rm{a}}^2}}}{\rm{ (3)}}\end{array}\)
Từ (1), (2) và (3) ta có:
\(\begin{array}{l}k\frac{{\left| {q{q_0}} \right|}}{{{a^2}}}2 = k\frac{{{q^2}}}{{{a^2}}}\sqrt 2 + k\frac{{{q^2}}}{{2{{\rm{a}}^2}}}\\ \to \left| {{q_0}} \right| = \frac{q}{2}(\sqrt 2 + \frac{1}{2}) = 2,{87.10^{ - 7}}C\\ \to {q_0} = - 2,{87.10^{ - 7}}C\end{array}\)
Hướng dẫn giải:
+ Áp dụng điều kiện cân bằng của vật
+ Áp dụng biểu thức định luật Cu-lông
+ Sử dụng phương pháp tổng hợp lực
+ Áp dụng hệ thức trong tam giác
