Bài 14: Phương trình tốc độ phản ứng và hằng số tốc độ phản ứng
Sách chân trời sáng tạo
Đơn vị của tốc độ phản ứng có thể là
\(Tốc\,\,độ\,\,phản\,\,ứng = \dfrac{{Nồng\,\,độ}}{{Thời\,\,gian\,\,phản\,\,ứng}}\)
=> Đơn vị của tốc độ = (Đơn vị của nồng độ):(Đơn vị của thời gian)=\(\dfrac{{mol}}{{l.h}} = mol.{l^{ - 1}}.{h^{ - 1}}\)
Cho phương trình phản ứng tổng hợp phosgene (COCl2) là một chất độc hóa học được sử dụng trong chiến tranh thế giới thứ nhất sau:
\(CO + C{l_2} \to COC{l_2}\)
Phương trình tốc độ phản ứng được xác định từ thực nghiệm có dạng như sau:
\(v = k.{C_{CO}}.C_{C{l_2}}^{3/2}\)
Tốc độ phản ứng thay đổi như thế nào nếu tăng nồng độ Cl2 lên 3 lần?
Gọi nồng độ ban đầu của CO và Cl2 lần lượt là \({C_{CO}}\)và \({C_{C{l_2}}}\)=> \(v = k.{C_{CO}}.C_{C{l_2}}^{3/2}\)
Khi tăng nồng độ Cl2 lên 3 lần tức có \(3{C_{C{l_2}}}\)=> \(v' = k.{C_{CO}}.{(3{C_{C{l_2}}})^{3/2}} \simeq 5,2k{C_{CO}}.C_{C{l_2}}^{3/2} = 5,2v\)
=> Khi tăng nồng độ Cl2 lên 3 lần thì tốc độ phản ứng tăng lên khoảng 5,2 lần
Cho phương trình phản ứng sau: \(2NO + {O_2} \to 2N{O_2}\). Từ thực nghiệm, biểu thức tốc độ phản ứng có dạng: \(v = k.C_{NO}^2.{C_{{O_2}}}\). Tốc độ phản ứng thay đổi như thế nào nếu tăng nồng độ NO lên 2 lần?
Gọi nồng độ ban đầu của NO và O2 lần lượt là \({C_{NO}}\)và \({C_{{O_2}}}\)=> \(v = k.C_{NO}^2.{C_{{O_2}}}\)
Khi tăng nồng độ NO lên 2 lần tức có \(2{C_{NO}}\)=> \(v' = k.{(2{C_{NO}})^2}.{C_{{O_2}}} = 4k.C_{NO}^2.{C_{{O_2}}} = 4v\)
=> Khi tăng nồng độ NO lên 2 lần thì tốc độ phản ứng tăng 4 lần
Ở 35oC tốc độ một phản ứng là 0,036 mol.l-1.h-1. Ở 45oC tốc độ phản ứng đó là 0,09 mol.l-1.h-1. Hệ số nhiệt độ Van’t Hoff của phản ứng là
Ta có t2=45oC, t1=35oC
Áp dụng công thức: \(\dfrac{{{v_{{t_2}}}}}{{{v_{{t_1}}}}} = {\gamma ^{\dfrac{{{t_2} - {t_1}}}{{10}}}} \Leftrightarrow \dfrac{{0,09}}{{0,036}} = {\gamma ^{\dfrac{{45 - 35}}{{10}}}} = {\gamma ^1} = 2,5\)
Biểu thức tính tốc độ phản ứng là
\(Tốc\,\,độ\,\,phản\,\,ứng = \dfrac{{Nồng\,\,độ}}{{Thời\,\,gian\,\,phản\,\,ứng}}\)
Cho phương trình hóa học của phản ứng: \(2CO(g) + {O_2}(g) \to 2C{O_2}(g)\). Nếu hệ số nhiệt độ Van’t Hoff bằng 2, tốc độ phản ứng thay đổi như thế nào khi giảm nhiệt độ của phản ứng từ 80oC xuống 50oC?
Ta có t2=50oC, t1=80oC
Áp dụng công thức: \(\dfrac{{{v_{{t_2}}}}}{{{v_{{t_1}}}}} = {\gamma ^{\dfrac{{{t_2} - {t_1}}}{{10}}}} = {2^{\dfrac{{50 - 80}}{{10}}}} = {2^{ - 3}} = 1/8\)
Tốc độ phản ứng giảm 8 lần khi giảm nhiệt độ của phản ứng từ 80oC xuống 50oC
Hằng số tốc độ phản ứng k được gọi là tốc độ riêng khi
Hằng số tốc độ phản ứng k được gọi là tốc độ riêng khi nồng độ tất cả các chất đầu đều bằng đơn vị.
Hằng số k phụ thuộc
Hằng số k chỉ phụ thuộc vào nhiệt độ, không phụ thuộc vào nồng độ chất phản ứng.
Trong một thí nghiệm, người ta đo được tốc độ trung bình của phản ứng của zinc (dạng bột) với dung dịch HCl là 0,005 mol/s. Nếu ban đầu cho 0,3 mol zinc dạng bột vào dung dịch HCl ở trên thì sau bao lâu còn lại 0,03 mol zinc?
Số mol zinc đã tan là 0,3 – 0,03 = 0,27 mol
Thời gian để hòa tan hết 0,27 mol zinc là \(\dfrac{{0,27}}{{0,005}} = 54\) giây
Cho đồ thị biểu diễn đường cong động học của phản ứng giữa oxygen và hydrogen tạo thành nước như sau:
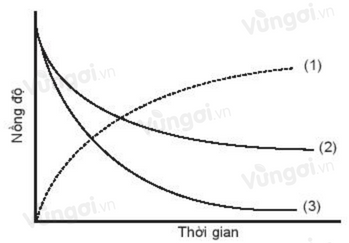
Đường cong nào là của oxygen?
PTHH: \({O_2} + 2{H_2} \to 2{H_2}O\)
Nhận thấy O2 và H2 là các chất tham gia phản ứng nên nồng độ theo thời gian sẽ giảm
Theo PTHH số phân tử O2 tham gia phản ứng ít hơn số phân tử H2 nên số va chạm hiệu quả với H2 để tạo thành H2O ít hơn => Sự giảm nồng độ theo thời gian của O2 chậm hơn so với H2 => Tương ứng với đường cong (2)
Cho phản ứng sau: \(3{I^ - }(aq) + {S_2}{O_8}^{2 - }(aq) \to {I_3}^ - (aq) + 2S{O_4}^{2 - }(aq)\). Kết quả nghiên cứu động học của phản ứng được cho trong bảng dưới đây:

Công thức tính tốc độ của phản ứng trên có dạng là
Theo định luật tác dụng khối lượng có: \(v = k.{[{I^ - }{\rm{]}}^a}.{{\rm{[}}{S_2}{O_8}^{2 - }{\rm{]}}^b}\)
Thay các giá trị tương ứng vào công thức trên ta được:
\({v_1} = k.{(0,001)^a}.{(0,001)^b}\)
\({v_2} = k.{(0,002)^a}.{(0,001)^b}\)
\({v_3} = k.{(0,002)^a}.{(0,002)^b}\)
=> \(\dfrac{{{v_2}}}{{{v_1}}} = {2^a} = 2 \Rightarrow a = 1\); \(\dfrac{{{v_3}}}{{{v_2}}} = {2^b} = 2 \Rightarrow b = 1\)
=> Biểu thức định luật tốc độ phản ứng là \(v = k.{\rm{[}}{I^ - }{\rm{]}}.{\rm{[}}{S_2}{O_8}^{2 - }{\rm{]}}\)
Xét phản ứng sau: \(HI + {C_2}{H_5}I \to {C_2}{H_6} + {I_2}\)
Phương trình tốc độ phản ứng có dạng: \(v = k.C_{HI}^x.C_{{C_2}{H_5}I}^y\)
Thực hiện phản ứng với nồng độ đầu khác nhau và đo tốc độ phản ứng tương ứng thu được kết quả trong bảng sau:

Thí nghiệm 1: \({v_1} = k.{(0,01)^x}.{(0,01)^y} = 1,{2.10^{ - 5}}\) (1)
Thí nghiệm 2: \({v_2} = k.{(0,01)^x}.{(0,02)^y} = 2,{4.10^{ - 5}}\) (2)
Thí nghiệm 3: \({v_3} = k.{(0,02)^x}.{(0,02)^y} = 4,{8.10^{ - 5}}\) (3)
Từ (1) và (2) => m = 1
Từ (2) và (3) => n = 1
Thay m = n = 1 vào (1) => k = 0,12 (L.mol-1.s-1)
Tốc độ phản ứng giữa KMnO4 và H2C2O4 có thể được xác định qua sự thay đổi màu của dung dịch do biến thiên nồng độ của ion MnO4-. Khi tiến hành phản ứng ở nhiệt độ không đổi 25oC, người ta thu được các số liệu sau:

Công thức tính tốc độ của phản ứng trên là
Biểu thức định luật tác dụng khối lượng: \(v = k.{{\rm{[}}{H_2}{C_2}{O_4}{\rm{]}}^a}.{{\rm{[}}Mn{O_4}^ - {\rm{]}}^b}\)
Thay số liệu trong bảng vào biểu thức trên ta có:
Thí nghiệm 1: \({v_1} = k.{{\rm{[}}1,98]^a}.{{\rm{[}}1,{08.10^{ - 2}}{\rm{]}}^b} = 5,{4.10^{ - 5}}\) (1)
Thí nghiệm 2: \({v_2} = k.{{\rm{[}}3,97]^a}.{{\rm{[}}1,{08.10^{ - 2}}{\rm{]}}^b} = 1,{1.10^{ - 4}}\) (2)
Thí nghiệm 3: \({v_3} = k.{{\rm{[}}1,98]^a}.{{\rm{[}}2,{17.10^{ - 2}}{\rm{]}}^b} = 2,{1.10^{ - 4}}\) (3)
Từ (1) và (2) suy ra a = 1
Từ (1) và (3) suy ra b = 2
=> Công thức tính tốc độ của phản ứng trên là \(v = k.{\rm{[}}{H_2}{C_2}{O_4}{\rm{]}}.{{\rm{[}}Mn{O_4}^ - {\rm{]}}^2}\)
Thả 1 mảnh magnesium có khối lượng 0,3 gam vào dung dịch HCl loãng. Sau 10 giây thấy mảnh magnesium tan hết. Tốc độ trung bình (mol/s) của phản ứng hòa tan magnesiumm là
Áp dụng công thức: \(\mathop v\limits^\_ = - \dfrac{{\Delta C}}{{\Delta t}} = - \dfrac{{0 - \dfrac{{0,3}}{{24}}}}{{10}} = 1,{25.10^{ - 3}}(mol/s)\)
Trong một thí nghiệm, người ta đo được tốc độ trung bình của phản ứng của zinc (dạng bột) với dung dịch HCl là 0,005 mol/s. Nếu ban đầu cho 0,5 mol zinc dạng bột vào dung dịch HCl ở trên thì sau bao lâu còn lại 0,05 mol zinc?
Số mol zinc đã tan là 0,5 – 0,05 = 0,45 mol
Thời gian để hòa tan hết 0,45 mol zinc là \(\dfrac{{0,45}}{{0,005}} = 90\) giây
Xét phản ứng phân hủy H2O2: \({H_2}{O_2} \to {H_2}O + 0,5{O_2}\)
Nghiên cứu sự thay đổi nồng độ một chất trong phản ứng theo thời gian, thu được đồ thị sau:
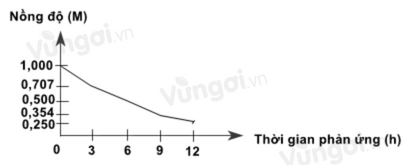
Đồ thị này mô tả sự thay đổi nồng độ theo thời gian của chất nào?
Từ đồ thị thấy nồng độ giảm theo thời gian => Chất phản ứng
=> Đồ thị trên mô tả sự thay đổi nồng độ H2O2 theo thời gian.
Cho phản ứng của các chất ở thể khí: \(2NO + {O_2} \to 2N{O_2}\)
Biểu thức nào sau đây không đúng?
NO2 là chất sản phẩm nên \({v_{tb}} = \dfrac{1}{2}.\dfrac{{\Delta {C_{N{O_2}}}}}{{\Delta t}}\) => D không đúng
Biểu thức tính hệ số nhiệt độ Van’t Hoff là
Biểu thức tính hệ số nhiệt độ Van’t Hoff là
\(\dfrac{{{v_{{t_2}}}}}{{{v_{{t_1}}}}} = {\gamma ^{\dfrac{{{t_2} - {t_1}}}{{10}}}}\)
Trong đó: \({v_{{t_1}}},{v_{{t_2}}}\)là tốc độ phản ứng ở 2 nhiệt độ t1 và t2
\(\gamma \) là hệ số nhiệt độ Van’t Hoff
Cho phản ứng xảy ra với khí độc CO: \(2CO\left( k \right){\rm{ }} + {\rm{ }}{O_2}\left( k \right) \to {\rm{ }}2C{O_2}\left( k \right)\). Biết hệ số nhiệt Van’t Hoff của phản ứng là \(\gamma \) = 2. Nếu tăng nhiệt độ của phản ứng từ 30oC lên 180oC thì tốc độ phản ứng tăng bao nhiêu lần?
Ta có t2=180oC, t1=30oC
Áp dụng công thức: \(\dfrac{{{v_{{t_2}}}}}{{{v_{{t_1}}}}} = {\gamma ^{\dfrac{{{t_2} - {t_1}}}{{10}}}} = {2^{\dfrac{{180 - 30}}{{10}}}} = {2^{15}} = 32768\)
Cho phản ứng của các chất ở thể khí: \(aA + bB \to cC\). Khi nồng độ A và B tăng lên 2 lần thì tốc độ phản ứng cũng tăng lên 2 lần. Tổng hệ số a+b là
Biểu thức tính vận tốc: \(v = k.C_A^a.C_B^b\)
Khi nồng độ A tăng 2 lần: \({v_1} = k.{(2{C_A})^a}.C_B^b = 2v\)
Khi nồng độ B tăng 2 lần: \({v_2} = k.C_A^a.{(2{C_B})^b} = 2v\)
=> \(k.{(2{C_A})^a}.C_B^b\)\( = k.C_A^a.{(2{C_B})^b}\)
Chọn giá trị của a, b sao cho thỏa mãn biểu thức trên => a=b=1 thỏa mãn

