Trả lời bởi giáo viên
Đáp án đúng: b
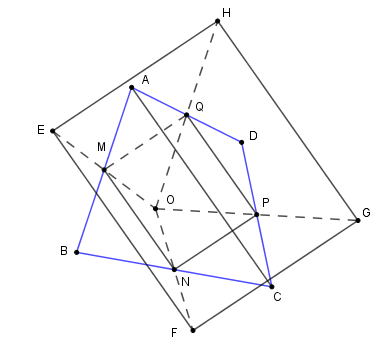
Vì \(E,F,F,H\) theo thứ tự là điểm đối xứng với \(O\) qua \(M,N,P,Q\) nên \(M,N,P,Q\) lần lượt là trung điểm của các đoạn thẳng \(OE;OF;OH;OG.\)
Xét tam giác \(OEF\) có \(MN\) là đường trung bình nên \(MN//EF;\,\,EF = 2MN\) (*)
Xét tam giác \(OHG\) có \(QP\) là đường trung bình nên \(QP//HG;\,HG = 2QP\) (**)
Mà \(MN = QP\) (theo câu trước) nên từ (*) và (**) suy ra \(EF//HG;\,EF = HG\).
Tứ giác \(EFGH\) có \(EF//HG;\,EF = HG\) nên \(EFGH\) là hình bình hành (dhnb).
Hướng dẫn giải:
Sử dụng tính chất đường trung bình của tam giác để suy ra cặp cạnh song song và bằng nhau.
Sử dụng dấu hiệu tứ giác có cặp cạnh đối song song và bằng nhau.

