Trả lời bởi giáo viên
Đáp án đúng: b
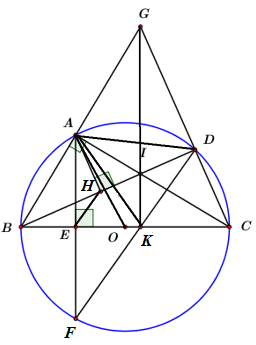
Ta có: \(\angle BAC,\)\(\angle BDC\) là góc nội tiếp chắn nửa đường tròn \(\left( O \right)\)\( \Rightarrow \angle BAC = \angle BDC = {90^0}.\)
\( \Rightarrow \angle GAI = \angle GDI = {90^0}\)
Xét tứ giác \(AIDG\) ta có: \(\angle GAI + \angle GDI = {90^0} + {90^0} = {180^0}\)
Suy ra \(AIDG\) là tứ giác nội tiếp đường tròn đường kính \(GI\).
Hướng dẫn giải:
Tứ giác có tổng hai góc đối bằng \({180^0}\) là tứ giác nội tiếp: chứng minh \(\angle GAI + \angle GDI = {180^0}\)\(\angle ABC\) là tứ giác nội tiếp

