Trong không gian toạ độ \(Oxyz\) cho đường thẳng \(d:\dfrac{{x - 1}}{2} = \dfrac{{y - 2}}{2} = \dfrac{z}{1}\) và hai điểm \(A\left( {1; - 1;1} \right),\,B\left( {4;2; - 2} \right)\). Gọi \(\Delta \) là đường thẳng đi qua \(A\) và vuông góc với \(d\) sao cho khoảng cách từ điểm \(B\) đến \(\Delta \) là nhỏ nhất. Phương trình của đường thẳng \(\Delta \) là

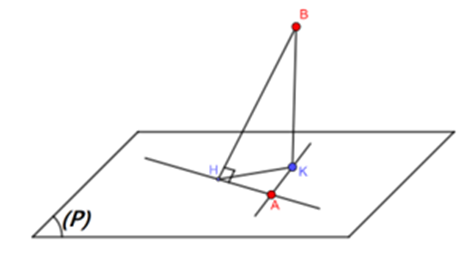
Vì \(\Delta \) là đường thẳng đi qua \(A\) và vuông góc với \(d\,\, \Rightarrow \Delta \) nằm trên mặt phẳng \(\left( P \right)\) qua \(A\) và vuông góc với \(d\).

Phương trình mp\(\left( P \right)\) là: \(2\left( {x - 1} \right) + 2\left( {y + 1} \right) + 1\left( {z - 1} \right) = 0\)\( \Leftrightarrow 2x + 2y + z - 1 = 0\).

Dựng \(BK \bot \left( P \right),\,BH \bot \Delta \,\,\left( {K \in \left( P \right),\,\,H \in \Delta } \right)\).

Phương trình đường thẳng \(BK\) là: \(\left\{ \begin{array}{l}x = 4 + 2t\\y = 2 + 2t\\z =  - 2 + t\end{array} \right.\).

Giả sử: \(K\left( {4 + 2t;2 + 2t;t - 2} \right) \in BK\).

Vì \(K \in \left( P \right)\) \( \Rightarrow 2\left( {4 + 2t} \right) + 2\left( {2 + 2t} \right) + (t - 2) - 1 = 0\) \( \Leftrightarrow 9t + 9 = 0 \Leftrightarrow t =  - 1\).

\( \Rightarrow K\left( {2;0; - 3} \right)\).

Ta thấy: \(BH \ge BK\) (quan hệ đường vuông góc, đường xiên).

Do đó, khoảng cách từ điểm \(B\) đến \(\Delta \) là \(BH\) đạt giá trị nhỏ nhất \( \Leftrightarrow BH = BK \Leftrightarrow H \equiv K\).

Khi đó, \(\Delta \) là đường thẳng đi qua \(A\left( {1; - 1;1} \right)\) và \(K\left( {2;0; - 3} \right)\).

Ta có: \(\overrightarrow {AK}  = \left( {1;1; - 4} \right)\) là 1 VTCP của đường thẳng \(\Delta \).

Phương trình đường thẳng \(\Delta \) đi qua \(A\left( {1; - 1;1} \right)\) và có 1 VTCP \(\overrightarrow {AK}  = \left( {1;1; - 4} \right)\) là: \(\dfrac{{x - 1}}{1} = \dfrac{{y + 1}}{1} = \dfrac{{z - 1}}{{ - 4}}\).