Câu hỏi:
3 năm trước
Trên tia phân giác góc ngoài tại đỉnh \(C\) của tam giác \(ABC,\) lấy điểm \(M\) (\(M\) khác \(C\)). Chọn câu đúng.
Trả lời bởi giáo viên
Đáp án đúng: b
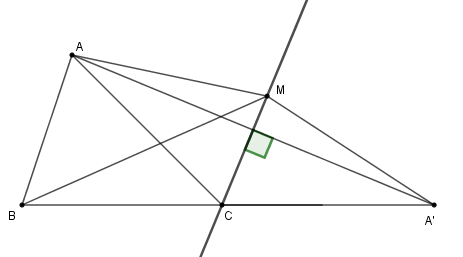
Trên tia đối của tia \(CB\) lấy điểm \(A'\) sao cho \(CA = CA'\)
Khi đó ta có: \(\Delta CAA'\) cân tại \(C\) có \(CM\) là phân giác \(\widehat {ACA'}\) nên \(CM\) cũng là đường trung trực của \(AA'\).
Từ đó ta có: \(MA = MA'\)
Nên \(MA + MB = MA' + MB\).
Xét tam giác \(MA'B\) có \(MA' + MB > A'B \Leftrightarrow MA + MB > A'C + BC\)
Hay \(MA + MB > AC + BC\) (vì \(CA = CA'\)).
Hướng dẫn giải:
+ Sử dụng tính chất đường trung trực của đoạn thẳng.
+ Sử dụng bất đẳng thức về ba cạnh của tam giác: Cho tam giác \(ABC\) thì \(\left| {AB - AC} \right| < BC < AB + AC\).