Câu hỏi:
2 năm trước
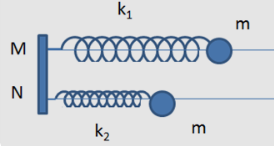
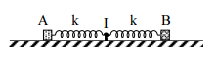
Trên mặt phẳng nằm ngang có hai con lắc lò xo. Các lò xo có cùng độ cứng k, cùng chiều dài tự nhiên là \(16cm\). Các vật nhỏ A và B có khối lượng lần lượt là \(m\) và \(4m\). Ban đầu, A và B được giữ ở vị trí sao cho lò xo gắn với A bị dãn \(4cm\) còn lò xo gắn với B bị nén \(4cm\). Đồng thời thả nhẹ để hai vật dao động điều hòa trên cùng một đường thẳng đi qua giá I cố định (hình vẽ). Trong quá trình dao động, khoảng cách lớn nhất và nhỏ nhất giữa hai vật có giá trị lần lượt là:
Trả lời bởi giáo viên
Đáp án đúng: b
+ Tần số góc của của con lắc B: \({\omega _2} = \sqrt {\frac{k}{{4m}}} = \omega \), con lắc A: \({\omega _1} = \sqrt {\frac{k}{m}} = 2\omega \)
+ Phương trình dao động của vật A là \({x_1} = 4\cos (2\omega t + \pi )\)
Phương trình dao động của vật B là \({x_2} = 4\cos (\omega t + \pi )\)
Mặt khác:
\(\begin{array}{l}AI = 16 - {x_1};BI = 16 + {x_2}\\ \to AB = 32 + {x_2} - {x_1}\end{array}\)
Ta có:
\(\begin{array}{l}d = {x_2} - {x_1} = 4\cos (\omega t + \pi ) - 4\cos (2\omega t + \pi )\\ = - 4cos\left( {\omega t} \right) + 4cos\left( {2\omega t} \right)\\ = 4\left( {cos2\omega t - cos\omega t} \right)\end{array}\)
Đặt: \(\cos \omega t = a\)
\(\begin{array}{l} \to d = 4(\cos 2\omega t - \cos \omega t)\\ = 4(2{a^2} - a - 1)\end{array}\)
Xét:
\(\begin{array}{l}f(a) = 2{a^2} - a - 1/\left( { - 1;1} \right)\\f' = 4a - 1\\f' = 0 \leftrightarrow a = \frac{1}{4}\end{array}\)
Xét bảng biến thiên sau
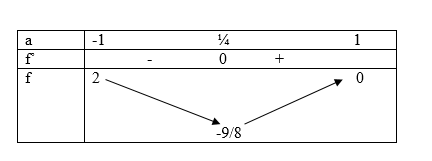
Từ bảng biến thiên ta có:
\(\begin{array}{l} - \frac{9}{8} \le f(a) \le 2\\ \to AB = 32 + d\\ \to 32 + 4.\left( { - \frac{9}{8}} \right) \le AB \le 32 + 4.2\\ \to 27,5 \le AB \le 40\end{array}\)
Hướng dẫn giải:
+ Sử dụng biểu thức tính tần số góc: \(\omega = \sqrt {\frac{k}{m}} \)
+ Viết phương trình dao động của mỗi con lắc
+ Sử dụng lí thuyết về khoảng cách của hai vật dao động điều hoà
+ Khảo sát hàm số bậc hai
Câu hỏi khác
- Bài tập lí thuyết dao động điều hòa có lời giải MÔN LÝ lớp 12
- Bài tập xác định thời gian vật chuyển động từ x1 đến x2, số lần qua li độ x có lời giải MÔN LÝ lớp 12
- Bài tập các đại lượng đặc trưng của DĐĐH có lời giải MÔN LÝ lớp 12
- Bài tập xác định quãng đường, tốc độ trung bình của vật trong DĐĐH có lời giải MÔN LÝ lớp 12
- Bài tập viết phương trình dao động điều hòa có lời giải MÔN LÝ lớp 12
