Trên mặt nước có hai nguồn kết hợp \(A\),\(B\) cách nhau \(40cm\) dao động theo phương trình \({u_A} = 5c{\rm{os}}\left( {24\pi t + \pi } \right)mm\) và \({u_B} = 5c{\rm{os}}\left( {24\pi t} \right)mm\). Tốc độ truyền sóng là \(v = 48cm/s\). Coi biên độ sóng không đổi khi sóng truyền đi. Xét các điểm trên mặt nước thuộc đường tròn tâm \(I\), bán kính \(R = 5cm\), điểm \(I\) cách đều \(A\) và \(B\) một đoạn \(25cm\). Điểm \(M\) trên đường tròn đó cách \(A\) xa nhất dao động với biên độ bằng:
Trả lời bởi giáo viên
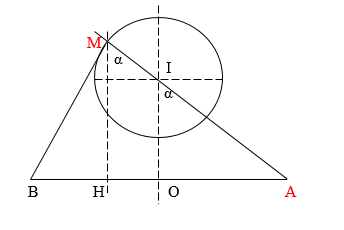
Phương trình sóng tại M do A truyền tới:
\({u_{1M}} = 5c{\rm{os}}\left( {24\pi \left( {t - \dfrac{{{d_1}}}{v}} \right) + \pi } \right)\)
Phương trình sóng tại M do B truyền tới:
\({u_{2M}} = 5c{\rm{os}}24\pi \left( {t - \dfrac{{{d_2}}}{v}} \right)\)
Phương trình sóng tại M là \({u_M} = {\text{ }}{u_{1M}} + {\text{ }}{u_{2M}}\)
Biên độ sóng tại M là:
\({A_M} = 10\left| {c{\rm{os}}\left( {\dfrac{{\pi \left( {{d_1} - {d_2}} \right)}}{4} - \dfrac{\pi }{2}} \right)} \right|{\rm{ (1)}}\)
Điểm I cách đều A và B nên I thuộc đường trung trực của AB
Có \(O{I^2} = {\text{ }}I{A^2} - {\text{ }}O{A^2} = {\text{ }}{25^2} - {\text{ }}{20^2} = {\text{ }}225\)
Suy ra \(OI = 15 cm\)
Có \(AM = 30cm\) (2) ( Chứng minh M, I, A thẳng hàng)
Lại có \(\sin \alpha = \dfrac{{OA}}{{AI}} = \dfrac{{20}}{{25}} = \dfrac{4}{5}\)
Suy ra \(cos\alpha = \sqrt {1 - {{\left( {\dfrac{4}{5}} \right)}^2}} = \dfrac{3}{5}\)
Mặt khác: \(\sin \alpha = \dfrac{{HA}}{{AM}} \to HA = AM.\sin \alpha = 30.\dfrac{4}{5} = 24cm\)
Nên \(BH = AB - HA = 40 - 24 = 16cm\); \(cos\alpha = \dfrac{{HM}}{{AM}} \to HM = AM.cos\alpha = 30.\dfrac{3}{5} = 18cm\)
Trong tam giác \(BMH\) có \(B{M^2} = B{H^2} + {\text{ }}M{H^2} = {16^2} + {\text{ }}{18^2} = {\text{ }}580\)
Vậy \(BM = \sqrt {580} cm{\rm{ }}\left( 3 \right)\)
Thay (2) và (3) vào (1) ta có: \({A_M} = 10\left| {c{\rm{os}}\left( {\dfrac{{\pi \left( {30 - \sqrt {580} } \right)}}{4} - \dfrac{\pi }{2}} \right)} \right|\)
\({A_M} = 10\left| {cos\left( {\dfrac{{\left( {30 - \sqrt {580} } \right)\pi }}{4} - \dfrac{\pi }{2}} \right)} \right| = 9,98mm\)
Hướng dẫn giải:
+ Viết phương trình sóng dao động tại M: $u_M= u_{1M}+u_{2M}$
+ \(M\) thuộc đường tròn cách \(A\) xa nhất khi \(M, I, A\) thẳng hàng
+ Áp dụng biểu thức tính biên độ dao động tại \(M\)

