Trên bề mặt chất lỏng có hai nguồn kết hợp AB cách nhau \(32cm\) dao động cùng pha. Biết sóng do mỗi nguồn phát ra có tần số \(f = 12\left( {Hz} \right)\), vận tốc truyền sóng \(2,4\left( {m/s} \right)\). Gọi M là một điểm nằm trên đường vuông góc với AB tại A dao đông với biên độ cực đại. Đoạn AM có giá trị lớn nhất là :
Trả lời bởi giáo viên
Ta có \(\lambda = \frac{v}{f} = \frac{{2,4}}{{12}} = 0,2m = 20(cm)\).
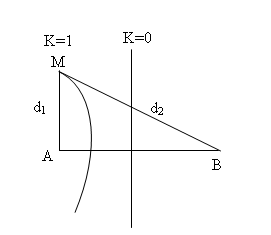
Do M là một cực đại giao thoa nên để đoạn AM có giá trị lớn nhất thì M phải nằm trên vân cực đại bậc 1 như hình vẽ và thõa mãn:
\({d_2} - {d_1} = k\lambda = 1.20 = 20(cm)\) (1) (lấy k = +1)
Mặt khác, do tam giác AMB là tam giác vuông tại A nên ta có :
\(BM = {d_2} = \sqrt {(A{B^2}) + (A{M^2})} = \sqrt {{{32}^2} + {d_1}^2} \) (2)
Thay (2) vào (1) ta được :
\(\begin{array}{l}\sqrt {{{32}^2} + {d_1}^2} - {d_1} = 20\\ \leftrightarrow \sqrt {{{32}^2} + d_1^2} = 20 + {d_1}\\ \leftrightarrow {32^2} + d_1^2 = {20^2} + 40{d_1} + d_1^2\\ \to {d_1} = 15,6cm\end{array}\)
Hướng dẫn giải:
+ Áp dụng biểu thức xác định bước sóng: \(\lambda = \frac{v}{f}\)
+ Áp dụng điều kiện dao động cực đại của 2 nguồn cùng pha: \({d_2} - {\rm{ }}{d_1} = {\rm{ }}k\lambda \)

