Trả lời bởi giáo viên
Đáp án đúng: c
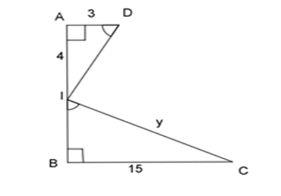
Áp dụng định lý Pitago trong tam giác vuông IAD ta có:
\(\begin{array}{l}\;\;\;\;A{I^2} + A{D^2} = I{D^2}\;\;\\ \Leftrightarrow {4^2} + {3^2} = I{D^2}\\ \Leftrightarrow I{D^2} = 25\\ \Rightarrow ID = 5\end{array}\)
Xét 2 tam giác vuông IAD và CBI có: \(\widehat {IDA} = \widehat {CIB}\;(gt)\)
\( \Rightarrow \Delta IAD \backsim \Delta CBI\;(g - g)\)
\( \Rightarrow \dfrac{{IA}}{{CB}} = \dfrac{{ID}}{{CI}}\)\( \Leftrightarrow \dfrac{4}{{15}} = \dfrac{5}{y} \Leftrightarrow y = \dfrac{{15.5}}{4} = 18,75\)
Vậy \(y = 18,75\).
Hướng dẫn giải:
- Tính \(ID\) theo Pytago
- Áp dụng các phương pháp chứng minh tam giác đồng dạng để tìm ra cặp tam giác đồng dạng phù hợp.
- Suy ra tỉ lệ thức phù hợp, biến đổi tỉ lệ thức để tính giá trị của $x.$