Câu hỏi:
2 năm trước
Tìm trên trục hoành điểm $P$ sao cho tổng khoảng cách từ $P$ tới hai điểm $A$ và $B$ là nhỏ nhất, biết \(A\left( {1;2} \right)\) và \(B\left( {3;4} \right)\)
Trả lời bởi giáo viên
Đáp án đúng: a
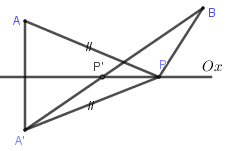
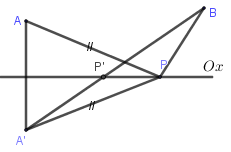
Dễ thấy $A,B$ cùng phía với trục hoành.
Gọi $A'$ là điểm đối xứng với $A$ qua trục hoành, suy ra \(A'\left( {1; - 2} \right)\) và \(PA = PA'\)
Ta có \(PA + PB = PA' + PB \ge A'B\). Dấu bằng xảy ra \( \Leftrightarrow \overrightarrow {A'P} \) cùng phương với \(\overrightarrow {A'B} \)
Suy ra \(\dfrac{{{x_P} - 1}}{{3 - 1}} = \dfrac{{0 + 2}}{{4 + 2}} \Rightarrow {x_P} = \dfrac{5}{3} \Rightarrow P\left( {\dfrac{5}{3};0} \right)\)
Hướng dẫn giải:
Nhận xét vị trí của \(A,B\) so với trục hoành, từ đó đánh giá giá trị nhỏ nhất của \(PA + PB\) dựa vào vị trí của \(P\)
