Câu hỏi:
2 năm trước
Tìm tập giá trị nhỏ nhất, giá trị lớn nhất của hàm số sau
\(y = 3{\left( {3\sin x + 4\cos x} \right)^2} + 4\left( {3\sin x + 4\cos x} \right) + 1\)
Trả lời bởi giáo viên
Đáp án đúng: c
Đặt \(t = 3.\sin x + 4.\cos x\), theo bất đẳng thức Bunhiacopxki, ta có:
$\begin{array}{l}
{t^2} = {\left( {3\sin x + 4\cos x} \right)^2}\\
\le \left( {{3^2} + {4^2}} \right)\left( {{{\sin }^2}x + {{\cos }^2}x} \right)\\
= 25.1 = 25\\
\Rightarrow {t^2} \le 25 \Rightarrow - 5 \le t \le 5
\end{array}$
Xét hàm số \(y = 3{t^2} + 4t + 1 \) trên \([-5;5]\).
Hàm số \(y = 3{t^2} + 4t + 1 \) là hàm bậc hai có:
$\begin{array}{l}
- \frac{b}{{2a}} = - \frac{2}{3} \in \left[ { - 5;5} \right]\\
y\left( { - \frac{2}{3}} \right) = - \frac{1}{3}\\
y\left( { - 5} \right) = 56\\
y\left( 5 \right) = 96
\end{array}$
Ta có bảng biến thiên:
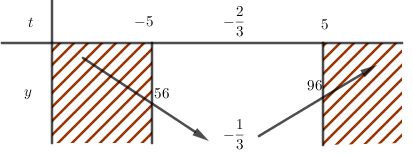
\( \Rightarrow \min y = - \dfrac{1}{3}\) khi \(t=- \dfrac{1}{3}\)
\(\max y = 96\) khi \(t=5\).
Hướng dẫn giải:
- Đặt \(t = 3.\sin x + 4.\cos x\) và tìm điều kiện của \(t\).
- Tìm GTNN của hàm số theo \(t\) và kết luận.
