Tam giác \(ABC\) vuông tại \(A\) có đường cao \(AH\). Cho biết \(AB = 3cm\); \(AC = 4cm\). Chọn kết luận không đúng.

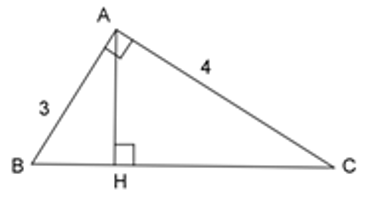
Áp dụng định lý Pytago vào tam giác vuông \(ABC\) ta có:

\(\begin{array}{l}A{B^2} + A{C^2} = B{C^2}\\ \Leftrightarrow {3^2} + {4^2} = B{C^2}\\ \Leftrightarrow B{C^2} = 25\\ \Rightarrow BC = 5\;cm\end{array}\)

Xét 2 tam giác vuông \(ABC\) và \(HBA\) có: \(\widehat B\) chung

\( \Rightarrow \Delta ABC\backsim\Delta HBA\;(g - g)\)

\( \Rightarrow \dfrac{{AB}}{{HB}} = \dfrac{{BC}}{{BA}} \Rightarrow HB = \dfrac{{A{B^2}}}{{BC}} = \dfrac{{{3^2}}}{5} = 1,8\;cm\)\( \Rightarrow HC = BC - HB = 5 - 1,8 = 3,2cm\)

Mặt khác:

\(\dfrac{{AB}}{{HB}} = \dfrac{{AC}}{{HA}} \Rightarrow HA = \dfrac{{AC.HB}}{{AB}} = \dfrac{{4.1,8}}{3} = 2,4\;cm\)

Nên \(HA = 2,4\,cm;\,HB = 1,8\,cm\), \(HC = 3,2cm,BC = 5cm\).