Câu hỏi:
2 năm trước
Tam giác \(ABC\) có \(AC = 2AB\), đường phân giác \(AD.\) Tính \(BD\) biết \(DC = 8cm.\)
Trả lời bởi giáo viên
Đáp án đúng: a
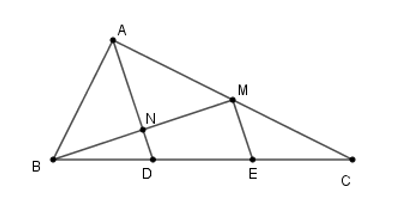
Gọi \(M,E\) lần lượt là trung điểm của \(AC,\,CD\).
Khi đó \(ME\) là đường trung bình của tam giác \(ACD \Rightarrow ME//AD\).
Gọi \(N\) là giao điểm của \(AD\) và \(BM.\)
Vì \(M\) là trung điểm của \(AC \Rightarrow AM = \dfrac{1}{2}AC\) mà \(AB = \dfrac{1}{2}AC\left( {gt} \right) \Rightarrow AB = AM\).
Suy ra tam giác \(ABM\) cân tại \(A\) có \(AN\) là phân giác (gt) nên \(AN\) cũng là đường trung tuyến của \(\Delta AMB\).
Hay \(NB = NM\)
Xét tam giác \(BME\) có \(NB = NM;\,ND//ME\) nên \(D\) là trung đểm của \(BE \Rightarrow BD = DE\).
Lại có: \(DE = \dfrac{1}{2}DC\) (do \(E\) là trung điểm \(DC\)) nên \(BD = \dfrac{1}{2}DC = \dfrac{1}{2}. 8 = 4cm.\)
Vậy \(BD = 4cm.\)
Hướng dẫn giải:
+ Gọi \(M,E\) là trung điểm \(AC,DC\).
+ Sử dụng tính chất, định lý về đường trung bình của tam giác.
+ Sử dụng tính chất tam giác cân.
