Ở mặt thoáng của một chất lỏng có hai nguồn kết hợp A, B cách nhau 10 cm, dao động theo phương thẳng đứng với phương trình lần lượt là uA = 3cos(40πt + π/6) cm; uB = 4cos(40πt + 2π/3) cm. Cho biết tốc độ truyền sóng là 40 cm/s. Một đường tròn có tâm là trung điểm của AB, nằm trên mặt nước, có bán kính R = 4cm. Số điểm dao động với biên độ 5 cm có trên đường tròn là:
Trả lời bởi giáo viên
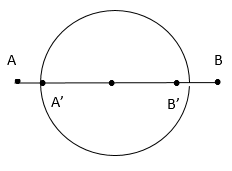
Bước sóng λ = v/f = 2 (cm)
Xét điểm M trên A’B’: d1 = AM; d2 = BM
Sóng truyền từ A, B đến M:
\({u_{AM}} = 3cos(10\pi t + \dfrac{\pi }{6} - \dfrac{{2\pi {d_1}}}{\lambda }) = 3cos(10\pi t + \dfrac{\pi }{6} - \pi {d_1}){\text{ (1)}}\)
\(\begin{gathered}{u_{BM}} = 4cos(10\pi t + \dfrac{{2\pi }}{3} - \dfrac{{2\pi {d_2}}}{\lambda }) = 4cos\left( {10\pi t + \dfrac{{2\pi }}{3} - \dfrac{{2\pi (10 - {d_1})}}{\lambda }} \right) = 4cos(10\pi t + \dfrac{{2\pi }}{3} + \pi {d_1} - 10\pi ) \hfill \\ = 4cos(10\pi t + \dfrac{{2\pi }}{3} + \pi {d_1}){\text{ (2)}} \hfill \\\end{gathered} \)
uM = uAM + uBM có biên độ bằng 5 cm khi uAM và uBM vuông pha với nhau:
\(\dfrac{{2\pi }}{3} + \pi {d_1} - \dfrac{\pi }{6} + \pi {d_1} = \dfrac{\pi }{2} + k\pi \to {d_1} = \dfrac{k}{2}\)
\(1 \leqslant {d_1} = \dfrac{k}{2} \leqslant 9 \to 2 \leqslant k \leqslant 18\)
Như vậy trên A’B’ có 17 điểm dao động với biên độ 5 cm trong đó có điểm A’ và B’.
Suy ra trên đường tròn tâm O bán kính \(R = 4cm\) có 32 điểm dao động với biên độ \(5 cm\)
Do đó trên đường tròn có 32 điểm dao động với biện độ \(5 cm\).
Hướng dẫn giải:
- Áp dụng công thức tính bước sóng: $\lambda = \dfrac{v}{f}$
- Viết phương trình sóng tại 1 điểm bất kì trên A’B’

