Câu hỏi:
2 năm trước
Một vật dao động là tổng hợp của hai dao động điều hòa cùng phương, cùng tần số có phương trình lần lượt là \({x_1} = 20\cos \left( {\omega t - \pi } \right)\,\,\left( {cm} \right)\) và \({x_2} = {A_2}\cos \left( {\omega t - \frac{\pi }{3}} \right)\,\,\left( {cm} \right)\). Thay đổi A2 để biên độ dao động tổng hợp có giá trị nhỏ nhất, khi đó lệch pha giữa dao động tổng hợp và dao động thành phần x1 là
Trả lời bởi giáo viên
Đáp án đúng: b
Ta có giản đồ vecto:
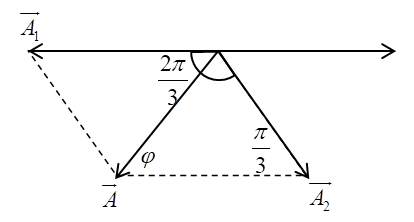
Từ giản đồ vecto, áp dụng định lí hàm cos, ta có:
\(\begin{array}{l}{A^2} = {A_1}^2 + {A_2}^2 + 2{A_1}{A_2}\cos \frac{{2\pi }}{3}\\ \Rightarrow {A^2} = {20^2} + {A_2}^2 - 20{A_2}\end{array}\)
Đặt \(x = {A_2}\), xét hàm số \(f\left( x \right) = {x^2} - 20x + {20^2}\), ta có:
\(f{'_{\left( x \right)}} = 2x - 20\)
Để \({A_{\min }} \Rightarrow {f_{\left( x \right)}}\min \Rightarrow f{'_{\left( x \right)}} = 0 \Rightarrow x = 10 \Rightarrow {A_2} = 10\,\,\left( {cm} \right)\)
Khi đó, \({A_{\min }} = 10\sqrt 3 \,\,\left( {cm} \right)\)
Ta có: \(\cos \varphi = \frac{{{A_1}^2 + {A^2} - {A_2}^2}}{{2A.{A_1}}} = \frac{{\sqrt 3 }}{2} \Rightarrow \varphi = \frac{\pi }{6}\)
Hướng dẫn giải:
Sử dụng giản đồ vecto
Định lí hàm cos: \({a^2} = {b^2} + {c^2} - 2bc\cos A\)
Câu hỏi khác
- Bài tập lí thuyết dao động điều hòa có lời giải MÔN LÝ lớp 12
- Bài tập xác định thời gian vật chuyển động từ x1 đến x2, số lần qua li độ x có lời giải MÔN LÝ lớp 12
- Bài tập các đại lượng đặc trưng của DĐĐH có lời giải MÔN LÝ lớp 12
- Bài tập xác định quãng đường, tốc độ trung bình của vật trong DĐĐH có lời giải MÔN LÝ lớp 12
- Bài tập viết phương trình dao động điều hòa có lời giải MÔN LÝ lớp 12
