Câu hỏi:
2 năm trước
Một vật dao động điều hòa với phương trình: \(x = 10c{\rm{os}}\left( {20\pi t - \dfrac{\pi }{6}} \right)cm\). Xác định thời điểm thứ $2016$ vật có gia tốc bằng không?
Một vật dao động điều hòa với phương trình: \(x = 10c{\rm{os}}\left( {20\pi t - \dfrac{\pi }{6}} \right)cm\). Xác định thời điểm thứ $2016$ vật có gia tốc bằng không?
Trả lời bởi giáo viên
Đáp án đúng: b
Ta có:
Chu kỳ: \(T = \frac{{2\pi }}{\omega } = \frac{{2\pi }}{{20\pi }} = 0,1s\)
\(\left\{ \begin{gathered}
a = - {\omega ^2}x \hfill \\
a = 0 \hfill \\
\end{gathered} \right. \to x = 0\)
Bài toán đưa về dạng xác định thời điểm vật qua li độ $x=0$ lần thứ $n$ ($n$ chẵn)
=> \({t_{2016}} = \frac{{2016 - 2}}{2}T + {t_2} = 1007T + {t_2}\)
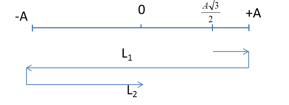
Tại $t=0$: \(\left\{ \begin{array}{l}x = 10c{\rm{os}}\left( {\dfrac{{ - \pi }}{6}} \right) = 5\sqrt 3 cm\\v = - 10.20\pi sin\left( {\dfrac{{ - \pi }}{6}} \right) = 100\pi > 0\end{array} \right.\)
$t_2$ là khoảng thời gian từ lúc bắt đầu đến khi qua $x=0$ lần thứ $2$
=> \({t_2} = \dfrac{T}{{12}} + \dfrac{{3T}}{4} = \dfrac{{5T}}{6}\)
\( \to {t_{2016}} = 1007T + {t_2} = 1007T + \dfrac{{5T}}{6} = \dfrac{{6047T}}{6} = \dfrac{{6047.0,1}}{6} = 100,783{\rm{s}}\)
Hướng dẫn giải:
+ Sử dụng công thức xác định chu kỳ $T$: \(T = \dfrac{{2\pi }}{\omega }\)
+ Sử dụng công thức xác định thời điểm vật đi qua li độ x lần thứ $n$ (với $n$ chẵn) : \(t = \dfrac{{n - 2}}{2}T + {t_2}\)
+ Xác định vị trí tại thời điểm $t=0 (x,v)$
Câu hỏi khác
- Bài tập lí thuyết dao động điều hòa có lời giải MÔN LÝ lớp 12
- Bài tập xác định thời gian vật chuyển động từ x1 đến x2, số lần qua li độ x có lời giải MÔN LÝ lớp 12
- Bài tập các đại lượng đặc trưng của DĐĐH có lời giải MÔN LÝ lớp 12
- Bài tập xác định quãng đường, tốc độ trung bình của vật trong DĐĐH có lời giải MÔN LÝ lớp 12
- Bài tập viết phương trình dao động điều hòa có lời giải MÔN LÝ lớp 12
