Một vật dao động điều hòa có đồ thị li độ theo thời gian như hình vẽ:
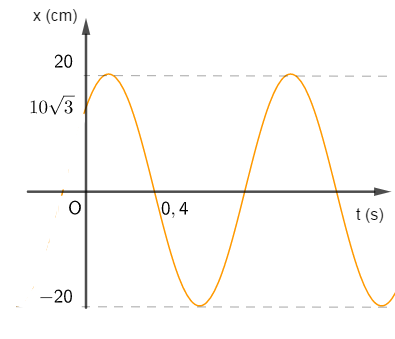
Kể từ lúc \(t = 0\) đến lúc vật đi qua vị trí \(x = - 10cm\) lần thứ 2015 theo chiều âm thì lực hồi phục sinh công dương trong thời gian:
Trả lời bởi giáo viên
+ Từ đồ thị, ta có:
- Biên độ dao động của vật \(A = 20cm\)
- Khoảng thời gian vật đi từ \(10\sqrt 3 \to 20 \to 0\) là: \(\Delta t = \dfrac{T}{{12}} + \dfrac{T}{4} = 0,4s \to T = 1,2s\)
- Tại thời điểm ban đầu, vật đang ở li độ \({\rm{?i}}\) và đang chuyển động theo chiều dương
+ Lực hồi phục luôn luôn hướng về VTCB, lực hồi phục sinh công dương khi vật chuyển động về VTCB và sinh công âm khi chuyện động ra VT biên.
+ Trong một chu kì, một nửa thời gian \(\left( {\dfrac{T}{2}} \right)\) lực hồi phục sinh công âm, một nửa thời gian \(\left( {\dfrac{T}{2}} \right)\) sinh công dương.
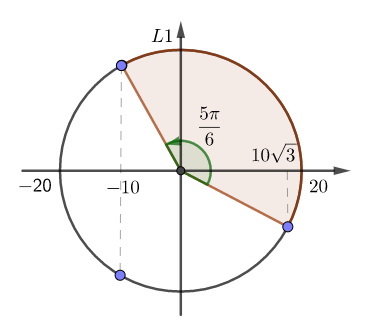
Dựa vào vòng tròn lượng giác, ta xác định được:
- Lần 1, vật qua li độ \(x = - 10cm\) theo chiều âm ứng với góc quét \(\dfrac{{5\pi }}{6}\).
Trong giai đoạn này khoảng thời gian sinh công dương là \(\dfrac{T}{4}\) ( ứng với cung phần tư thứ nhất).
- Để đến thời điểm lần thứ 2015, vật qua li độ \(x = - 10cm\) theo chiều âm thì cần quét thêm 2014 vòng và thời gian sinh công dương có thêm là \(2014\dfrac{T}{2} = 1007T\)
=> Tổng thời gian: \(\dfrac{T}{4} + 1007T = 1007,25T = 1007,25.1,2 = 1208,7s\)
Hướng dẫn giải:
+ Đọc đồ thị x – t, xác định các đại lượng:
- Biên độ dao động
- Chu kì dao động
- Vị trí tại thời điểm ban đầu
+ Lực hồi phục sinh công dương khi vật chuyển động về VTCB
+ Sử dụng vòng tròn lượng giác

