Một người đo chiều cao của cây nhờ 1 cọc chôn xuống đất, cọc cao 2,45 m và đặt xa cây 1,36 m. Sau khi người ấy lùi ra xa cách cọc 0,64 m thì người ấy nhìn thấy đầu cọc và đỉnh cây cùng nằm trên một đường thẳng. Hỏi cây cao bao nhiêu? Biết khoảng cách từ chân đến mắt người ấy là 1,65 m.

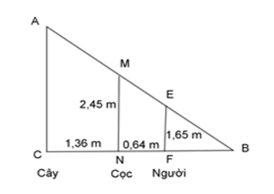
Ta mô tả vị trí cây, cọc và người như hình vẽ bên.

Xét \(\Delta BFE\) và \(\Delta BNM\) ta có:

\(\widehat B\;chung\)

\(\widehat {BEF} = \widehat {BMN}\) (vì \(EF//MN\), cặp góc đồng vị bằng nhau)

\( \Rightarrow \Delta BFE \backsim \Delta BNM\;(g - g)\)

\(\begin{array}{l} \Rightarrow \dfrac{{BF}}{{BN}} = \dfrac{{FE}}{{NM}} \Leftrightarrow \dfrac{{BF}}{{BF + FN}} = \dfrac{{FE}}{{NM}} \Leftrightarrow \dfrac{{BF}}{{BF + 0,64}} = \dfrac{{1,65}}{{2,45}}\\ \Leftrightarrow 1,65\left( {BF + 0,64} \right) = 2,45.BF\\ \Leftrightarrow BF = 1,32\;\;m.\end{array}\)

Xét \(\Delta BFE\) và \(\Delta BCA\) có:

\(\widehat B\;chung\)

\(\widehat {BEF} = \widehat {BAC}\) (vì $EF\parallel AC$, cặp góc đồng vị bằng nhau)

\( \Rightarrow \Delta BFE \backsim \Delta BCA\;(g - g)\)

\(\begin{array}{l} \Rightarrow \dfrac{{BF}}{{BC}} = \dfrac{{FE}}{{CA}} \Leftrightarrow \dfrac{{BF}}{{BF + FN + NC}} = \dfrac{{FE}}{{CA}} \Leftrightarrow \dfrac{{1,32}}{{1,32 + 0,64 + 1,36}} = \dfrac{{1,65}}{{CA}}\\ \Rightarrow CA = 4,15\;m\end{array}\) 

Vậy cây cao đúng bằng độ dài của đoạn CA hay cây cao 4,15 m.