Một lăng kính có góc chiết quang \(A = {6^0}\), chiết suất của lăng kính đối với tia đỏ \({n_d} = 1,64\) và đối với tia tím là \({n_t} = 1,68\). Chiếu tia sáng trắng tới mặt bên của lăng kính dưới góc tới rất nhỏ. Góc lệch giữa tia ló màu đỏ và tia tím ra khỏi lăng kính là:
Trả lời bởi giáo viên
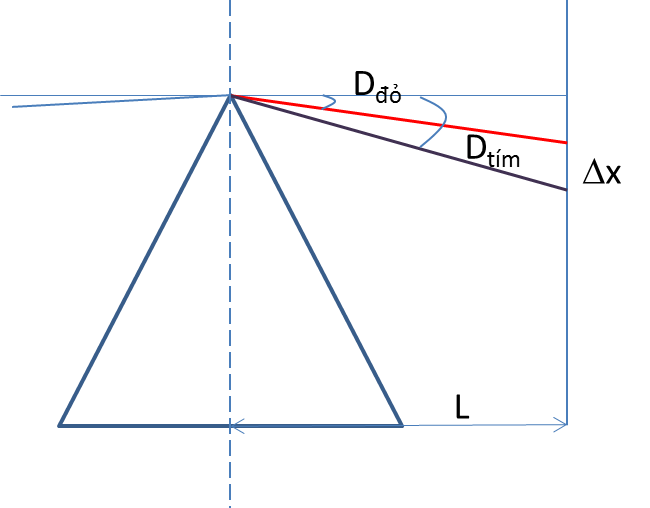
Ta có: \({{\mathop{\rm tanD}\nolimits} _d} = \dfrac{{{x_d}}}{L},{\rm{ }}{{\mathop{\rm tanD}\nolimits} _t} = \dfrac{{{x_t}}}{L}\)
Vì A≪ \( \to \left\{ \begin{array}{l}{D_d} \ll \\{D_t} \ll \end{array} \right. \to {\mathop{\rm tanD}\nolimits} \approx sinD \approx D\)
=> Góc lệch giữa tia ló màu đỏ và tia ló màu tím là: \(\Delta D = {D_t} - {D_d} = ({n_t} - 1)A - ({n_d} - 1)A = A({n_t} - {n_d}) = {6^0}(1,68 - 1,64) = {0,24^0}\)
Hướng dẫn giải:
Áp dụng công thức tính góc lệch khi góc chiết quang A nhỏ: \(D = \left( {n - 1} \right)A\)

