Một bể nước sâu \(1m\). Một chùm ánh sáng mặt trời chiếu vào mặt nước dưới góc tới \(i\) sao cho \(\sin i = 0,8\). Chiết suất của nước đối với ánh sáng đỏ là \(1,331\) và đối với ánh sáng tím là \(1,343\). Bề rộng của dải quang phổ dưới đáy bể là:
Trả lời bởi giáo viên
Ta có:
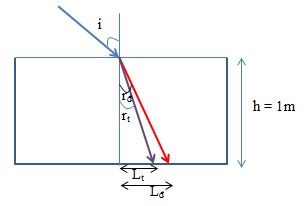
Theo định luật khúc xạ ánh sáng, ta có: \(\sin i = n{\mathop{\rm s}\nolimits} {\rm{inr}} \to \left\{ \begin{array}{l}{\mathop{\rm s}\nolimits} {\rm{in}}{{\rm{r}}_{\rm{d}}} = \dfrac{{\sin i}}{{{n_d}}} = \dfrac{{0,8}}{{1,331}} = 0,601\\{\mathop{\rm s}\nolimits} {\rm{in}}{{\rm{r}}_t} = \dfrac{{\sin i}}{{{n_t}}} = \dfrac{{0,8}}{{1,343}} = 0,597\end{array} \right. \to \left\{ \begin{array}{l}{r_d} = {36,942^0}\\{r_t} = {36,561^0}\end{array} \right.\)
Ta có: \(\left\{ \begin{array}{l}{L_d} = {\mathop{\rm t}\nolimits} {\rm{an}}{{\rm{r}}_d}.h = \tan {36,942^0}.1 = 0,7519m\\{L_t} = {\mathop{\rm t}\nolimits} {\rm{an}}{{\rm{r}}_t}.h = \tan {36,561^0}.1 = 0,7416m\end{array} \right.\)
Bề rộng của dải quang phổ dưới đáy bể: \(L = {L_d} - {L_t} = 0,7519 - 0,7416 = 0,01037m = 1,037cm\)
Hướng dẫn giải:
Áp dụng định luật khúc xạ ánh sáng: \(\sin i = n{\mathop{\rm s}\nolimits} {\rm{inr}}\)

