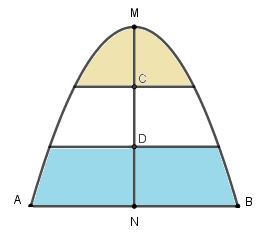
Một khung cửa kính hình parabol với đỉnh M và cạnh đáy AB như minh họa ở hình bên. Biết chi phí để lắp phần kính màu (phần tô đậm trong hình) là 200.000 đồng \(/{m^2}\) và phần kính trắng còn lại là 150.000 đồng \(/{m^2}\).Cho \(MN = AB = 4m\) và \(MC = CD = DN\). Hỏi số tiền để lắp kính cho khung cửa như trên gần nhất với số tiền nào dưới đây?

Công thức tính diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y = f\left( x \right)\), đường thẳng \(y = 0\) và hai đường thẳng \(x = a,x = b\left( {a < b} \right)\) là:

Công thức tính diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y = f\left( x \right) = {x^2} - 1\), trục hoành và hai đường thẳng \(x =  - 1;x =  - 3\) là:

Cho hàm số \(y=a{{x}^{4}}+b{{x}^{2}}+c\) ($a=1$) có đồ thị (C), biết rằng (C) đi qua \(A\left( -1;0 \right)\) , tiếp tuyến d tại A của (C) và hai đường thẳng \(x=0;x=2\) có diện tích bằng \(\dfrac{28}{5}\) (phần gạch chéo trong hình vẽ). Diện tích hình phẳng giới hạn bởi d, đồ thị (C) và hai đường thẳng \(x=-1;x=0\) có diện tích bằng

Cho parabol \(\left( P \right)\) có đồ thị như hình vẽ:

Tính diện tích giới hạn bởi \(\left( P \right)\) và trục hoành.

Tính diện tích hình phẳng giới hạn bởi đồ thị hai hàm số \(y={{x}^{2}}-2x\) và \(y=-{{x}^{2}}+4x\).

 Gọi (H) là hình phẳng giới hạn bởi đồ thị hàm số \(y={{x}^{2}}-4x+4\), trục tung và trục hoành. Xác định k để đường thẳng (d) đi qua điểm \(A\left( 0;4 \right)\) và có hệ số góc k chia (H) thành hai phần có diện tích bằng nhau.

Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y = {x^3}\), trục hoành và hai đường thẳng \(x = 1;\,\,x = 3\)?