Câu hỏi:
2 năm trước
Một khối thủy tinh P có chiết suất n = 1,5, tiết diện thẳng là một tam giác cân ABC vuông góc tại B. Chiếu vuông góc tới mặt AB một chùm sáng song song SI. Khối thủy tinh P ở trong nước có chiết suất n’ = 1,33. Tính góc D là góc hợp bởi tia ló và tia tới?
Trả lời bởi giáo viên
Đáp án đúng: a
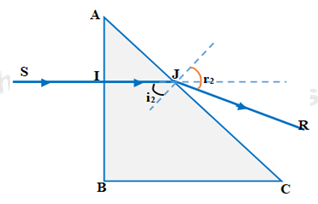
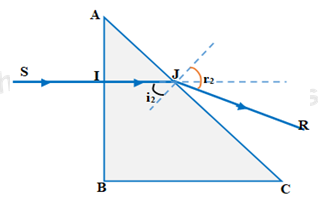
Tia tới SI ⊥ AB, góc tới i1 = 0 nên góc khúc xạ bằng r1 = 0, do đó tia SI truyền thẳng đến gặp mặt AC giữa thủy tinh và không khí, lúc này ta có trường hợp tia sáng đi từ thủy tinh ra nước.
Góc giới hạn igh tại mặt AC được tính theo công thức: \(\sin {i_{gh}}\; = \dfrac{{n'}}{n} = \dfrac{{1,33}}{{1,5}} \Rightarrow {i_{gh}}\; = 62,{46^0}\)
Tia SJ tới mặt AC với góc tới \({i_2}\; = {45^o}\; < {i_{gh}}\;\)nên cho tia khúc xạ ra mặt AC.
Áp dụng định luật khúc xạ tại mặt AC ta có:
\(\begin{array}{l}n.\sin {i_2}\; = n'.\sin {r_2}\\ \Rightarrow \sin {r_2} = \sin {i_2}.\dfrac{n}{{n'}} = \sin 45.\dfrac{{1,5}}{{1,33}} = 0,7975\\ \Rightarrow {r_2} = 52,{89^0}\end{array}\)
Góc D hợp bởi tia ló và tia tới là: \(D = {r_2}\;-{i_2}\; = 52,{89^0}{\rm{ - 4}}{{\rm{5}}^0} = 7,{89^0}\)
Hướng dẫn giải:
+ Định luật khúc xạ ánh sáng: \({n_1}\sin i = {n_2}\sin r\)
+ Điều kiện để có phản xạ toàn phần: \(\left\{ \begin{array}{l}{n_2} < {n_1}\\i \ge {i_{gh}};\,\,\left( {\sin {i_{gh}} = \dfrac{{{n_2}}}{{{n_1}}}} \right)\end{array} \right.\)
