Một con lắc lò xo, lò xo có độ cứng \(k = 80N/m\), vật M có khối lượng \(M = 350g\), dao động điều hòa trên mặt phẳng nằm ngang với biên độ \(2cm\). Khi M đang dao động thì có một vật có khối lượng \(m{\rm{ }} = 50g\) bắn vào M theo phương ngang với vận tốc \(1,2\sqrt 2 m/s\) . Giả thiết là va chạm mềm, xảy ra tại thời điểm lò xo có độ dài lớn nhất. Sau va chạm, hai vật gắn chặt vào nhau và cùng dao động điều hòa với biên độ là:
Trả lời bởi giáo viên
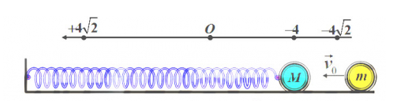
Ta có: \(\left\{ \begin{array}{l}\omega = \sqrt {\frac{k}{{m + M}}} = \sqrt {\frac{{80}}{{0,35 + 0,05}}} = 10\sqrt 2 ({\rm{r}}a{\rm{d}}/s)\\V = \frac{{m{v_0}}}{{m + M}} = \frac{{0,05.1,2\sqrt 2 }}{{0,05 + 0,35}} = \frac{{3\sqrt 2 }}{{20}}m/s = 15\sqrt 2 (cm/s)\end{array} \right.\)
Lại có: \(\left\{ \begin{array}{l}{x_0} = \pm 2cm\\A = \sqrt {x_0^2 + {{\frac{V}{{{\omega ^2}}}}^2}} = \sqrt {{2^2} + {{\left( {\frac{{15\sqrt 2 }}{{10\sqrt 2 }}} \right)}^2}} = 2,5cm\end{array} \right.\)
Hướng dẫn giải:
+ Vận dụng các công thức trong va chạm mềm của con lắc lò xo nằm ngang.
Va chạm mềm: \(m{v_0} = (m + M)V \Rightarrow V = \frac{1}{{1 + \frac{M}{m}}}{v_0}\)
V: vận tốc của hệ hai vật M+m ở vị trí cân bằng
+ Sử dụng hệ thức độc lập: \({A^2} = {x^2} + \frac{{{v^2}}}{{{\omega ^2}}}\)

